La méthode « Diviser pour régner » est un paradigme algorithmique puissant, souvent utilisé pour résoudre des problèmes complexes de manière élégante et efficace. L’idée est de décomposer un problème en plusieurs sous-problèmes, de les résoudre individuellement, puis de combiner leurs solutions pour obtenir la solution du problème initial.
Ce processus se décompose en trois phases principales :
- DIVISER : Le problème initial est scindé en plusieurs sous-problèmes plus petits, généralement de nature similaire à l’original.
- RÉGNER : Chaque sous-problème est résolu, souvent de manière récursive. La clé est que ces sous-problèmes sont plus simples à gérer que le problème de départ.
- COMBINER : Les solutions des sous-problèmes sont fusionnées pour construire la solution finale du problème d’origine.
Les algorithmes qui emploient cette approche sont très souvent de nature récursive. Un exemple classique de cette méthode est le tri-fusion.
Le Tri-Fusion
Présentation
Le tri-fusion est un algorithme de tri efficace qui repose sur le principe « Diviser pour régner ». Il prend un tableau non trié en entrée et renvoie le même tableau, mais cette fois, dans l’ordre croissant.
Voici une implémentation simplifiée en pseudo-code des deux fonctions qui composent cet algorithme : FUSION et TRI-FUSION.
VARIABLE
A : tableau d'entiers
L, R : tableaux d'entiers
p, q, r, n1, n2 : entiers
k, i, j : entiers
DEBUTFUSION (A, p, q, r):
n1 ← q - p + 1
n2 ← r - q
créer tableau L[1..n1+1] et R[1..n2+1]
pour i ← 1 à n1:
L[i] ← A[p+i-1]
fin pour
pour j ← 1 à n2:
R[j] ← A[q+j]
fin pour
L[n1+1] ← ∞
R[n2+1] ← ∞
i ← 1
j ← 1
pour k ← p à r:
si L[i] ⩽ R[j]:
A[k] ← L[i]
i ← i + 1
sinon:
A[k] ← R[j]
j ← j + 1
fin si
fin pour
fin FUSION
TRI-FUSION(A, p, r):
si p < r:
q = (p + r) / 2
TRI-FUSION(A, p, q)
TRI-FUSION(A, q+1, r)
FUSION(A, p, q, r)
fin si
fin TRI-FUSION
L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINER.
Un aspect intéressant du tri-fusion est que la phase de « Régner » est trivialement simple : le processus de division se poursuit jusqu’à ce que les sous-problèmes ne contiennent qu’un seul élément. Trier un tableau d’un seul élément ne demande aucune opération, ce qui simplifie grandement la tâche.
La véritable magie opère lors de la phase de fusion. Imaginons que nous ayons deux tableaux déjà triés, B et C, et que nous souhaitions les fusionner en un nouveau tableau T. On compare simplement le premier élément de B avec le premier de C, on ajoute le plus petit des deux à T, puis on recommence avec les éléments restants. On continue jusqu’à ce que l’un des tableaux soit vide, puis on ajoute les éléments restants de l’autre tableau à la fin de T.
Complexité
Bien que le calcul rigoureux soit hors de la portée de ce cours, nous pouvons en estimer la complexité de manière intuitive. La phase de division, où les tableaux sont coupés en deux à plusieurs reprises, est liée à la fonction logarithmique en base 2, soit log_2(n). La phase de fusion, pour un tableau de n éléments, nécessite un nombre de comparaisons proportionnel à n. En combinant ces deux observations, nous arrivons à une complexité approximative de l’ordre de O(nlog(n)).
Comme le montre la comparaison des courbes, un algorithme en O(nlog(n)) est beaucoup plus performant pour de grandes valeurs de n qu’un algorithme en O(n²), comme le tri par insertion ou le tri par sélection.
Retour sur la dichotomie
Présentation
C’est une méthode pour trouver un nombre N dans une liste triée si elle y est présente ou pour prouver son absence. Le principe est de regarder la valeur centrale, soit c’est celle qu’on cherche soit la valeur trouvée nous permettra de déterminer dans laquelle des sous listes de part et d’autre de la valeur devrait se situer N. Une fois fait on applique la même démarche sur la sous liste en question. On continuera jusqu’à soit tomber sur N ou obtenir une liste ne divise cette sous liste et on repère dans laquelle des parties devrait se situer la valeur. On continue, avec des sous listes de plus en plus petites et se dirigeant progressivement vers des listes vides. Soit on tombe sur N avant cela, sinon la valeur n’est pas présente. Cette recherche repose sur le principe « Diviser pour régner ».
exercice (corrigé ici)
compléter le code ci dessous
def recherche(t, v, g, d):
"""renvoie une position de v dans t[g..d],
supposé trié, et None si elle ne s’y trouve pas"""
if g > d:
return None
m = (g + d) // 2
if t[m] < v:
return recherche(t, v, m + 1, d)
elif t[m] > v:
return recherche(t, v, g, m - 1)
else:
return m
def recherche_dichotomique(t, v):
"""renvoie une position de v dans le tableau t,
supposé trié, et None si elle ne s’y trouve pas"""
return recherche(t, v, 0, len(t) - 1)
L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINE
Activités et Exercices
Activité 1
Appliquez l’algorithme de tri-fusion au tableau T= [23, 12, 4, 56, 35, 32, 42, 57, 3]. Vous pouvez créer un schéma et expliquer en détail la fusion de deux tableaux triés.
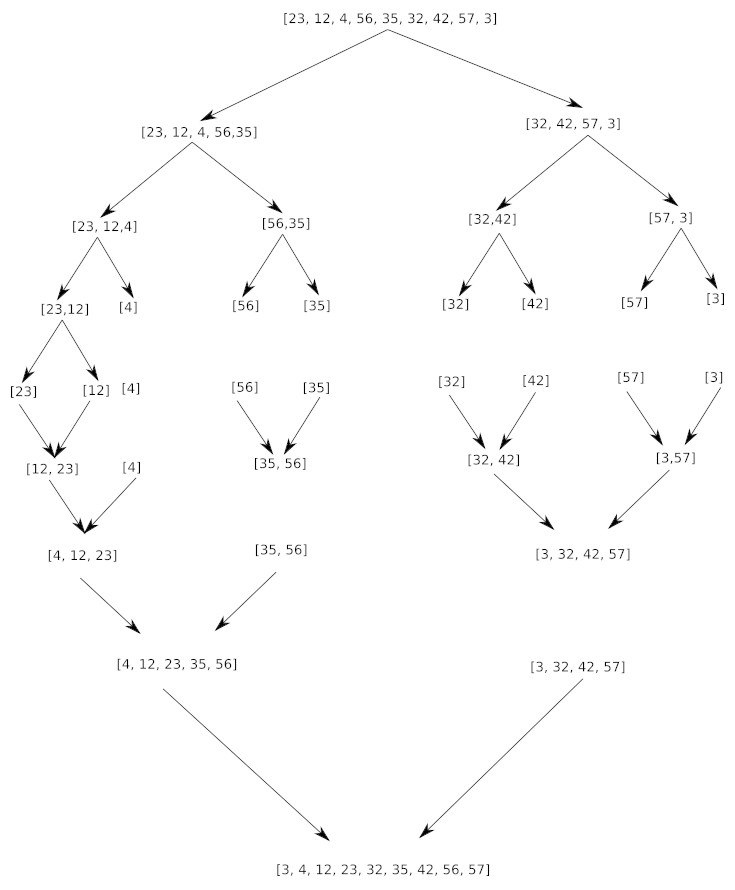
1. La phase de division
Le tri fusion commence par diviser de manière récursive le tableau initial en deux moitiés égales. Ce processus se poursuit jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément. À ce stade, le sous-tableau est considéré comme trié. C’est la partie « régner » de l’algorithme, qui est ici triviale.
2. La phase de fusion
Une fois que tous les sous-tableaux d’un seul élément sont formés, le tri fusion passe à la phase la plus importante : la fusion. L’idée est de fusionner deux sous-tableaux déjà triés en un seul grand tableau trié. C’est un processus simple qui se déroule en comparant les premiers éléments de chaque sous-tableau.
Prenons l’exemple de la fusion des deux tableaux triés suivants :
- B = [4, 12, 23, 35, 56]
- C = [3, 32, 42, 57]
Nous allons construire un nouveau tableau, T, qui contiendra le résultat de la fusion.
- On compare le premier élément de B (4) avec le premier élément de C (3). Comme 3 est plus petit que 4, on le place dans T.
- T = [3]
- B = [4, 12, 23, 35, 56]
- C = [32, 42, 57]
- On compare à nouveau le premier élément restant de B (4) avec le premier élément de C (32). Comme 4 est plus petit, on le place dans T.
- T = [3, 4]
- B = [12, 23, 35, 56]
- C = [32, 42, 57]
- On continue ce processus :
- On compare 12 et 32 : 12 est plus petit. On ajoute 12 à T.
- On compare 23 et 32 : 23 est plus petit. On ajoute 23 à T.
- On compare 35 et 32 : 32 est plus petit. On ajoute 32 à T.
- On compare 35 et 42 : 35 est plus petit. On ajoute 35 à T.
- On compare 56 et 42 : 42 est plus petit. On ajoute 42 à T.
- On compare 56 et 57 : 56 est plus petit. On ajoute 56 à T.
À ce stade, le tableau B est vide. Il ne reste plus qu’un seul élément dans C (57). On l’ajoute directement à la fin du tableau T.
- Le tableau final trié est donc : T = [3, 4, 12, 23, 32, 35, 42, 56, 57].
Ce processus de comparaison et d’ajout est répété pour toutes les fusions successives jusqu’à ce que tous les éléments soient rassemblés dans un seul tableau final trié.
Activité 2
Complétez le code Python suivant pour la fonction de tri-fusion :
def tri_fusion(tab):
def fusion(tab, p, q, r):
n1 = q-p+1
n2 = r-q
L = [0]*n1
R = [0]*n2
for i in range(n1):
L[i] = tab[p+i]
for j in range(n2):
R[j] = tab[q+j+1]
L.append(float("inf"))
R.append(float("inf"))
i = 0
j = 0
for k in range(p, r+1):
if L[i] <= R[j]:
tab[k] = L[i]
i = i + 1
else:
tab[k]=R[j]
j = j + 1
def tri_f(tab, p, r) :
if p < r:
q = (p + r) // 2
tri_f(tab, p, q)
tri_f(tab, q + 1, r)
fusion(tab, p, q, r)
tri_f(tab, p = 0, r = len(tab) - 1)
return tab
Activité 3
Complétez cette autre version du tri-fusion en Python, en utilisant le « slicing » :
def tri_fusion_slice(tab):
n = len(tab)
if n > 1:
mil = n // 2
L = tab[:mil]
R = tab[mil:]
tri_fusion_slice(L)
tri_fusion_slice(R)
i = 0
j = 0
k = 0
while i < len(L) and j < len(R):
if L[i] < R[j]:
tab[k] = L[i]
i += 1
else:
tab[k] = R[j]
j += 1
k += 1
while i < len(L):
tab[k] = L[i]
i += 1
k += 1
while j < len(R):
tab[k] = R[j]
j += 1
k += 1
Activité 4
En vous basant sur la vidéo disponible à cette adresse, implémentez l’algorithme de tri rapide (Quicksort) en Python, un autre algorithme basé sur le principe « Diviser pour régner ».
Exercices
- Exercice 1 : Donnez la séquence des appels à la fonction de recherche dichotomique du cours pour les appels
recherche_dichotomique([0,1,1,2,3,5,8,13,21], 13)etrecherche_dichotomique([0,1,1,2,3,5,8,13,21], 12). - Exercice 2 : Quelles sont les deux listes renvoyées par une fonction
coupe()à laquelle on passe la liste[8, 1, 3, 0, 1, 2, 5]? L’ordre relatif est-il préservé ? Est-ce important ? - Exercice 3 : Réécrivez la fonction
fusionen utilisant une bouclewhileau lieu de la récursivité. - Exercice 4 : Le problème des Tours de Hanoï est un jeu célèbre impliquant trois tiges et des disques de tailles différentes. Écrivez une fonction
hanoi(n)qui affiche la solution pour n disques. - Exercice 5 : Combien de déplacements élémentaires faut-il au total pour déplacer N disques de la tour de départ à la tour d’arrivée dans le problème des Tours de Hanoï ?
- Exercice 6 : Réécrivez l’exercice 4 en utilisant des piles (voir chapitre 5).
- Exercice 7 : Écrivez une fonction qui effectue la rotation d’une image de 90 degrés en utilisant le principe « Diviser pour régner ».
- Exercice 8 : Appliquez le principe « Diviser pour régner » pour multiplier deux entiers en utilisant la méthode de Karatsuba.
corrections
Exercice 1
- Pour
recherche_dichotomique([0,1,1,2,3,5,8,13,21], 13):recherche(t, 13, 0, 8)recherche(t, 13, 5, 8)recherche(t, 13, 7, 8)- À ce moment, l’index
mest 7, où se trouve la valeur 13.
- Pour
recherche_dichotomique([0,1,1,2,3,5,8,13,21], 12):recherche(t, 12, 0, 8)recherche(t, 12, 5, 8)recherche(t, 12, 7, 8)recherche(t, 12, 7, 6)- À ce moment, l’indice de gauche
gest supérieur à l’indice de droited, et la recherche se termine avec le résultatNone.
Exercice 2
Les deux listes renvoyées sont [5, 1, 3, 8] et [2, 0, 1]. L’ordre relatif des éléments est inversé, car la fonction ajoute les éléments au début des nouvelles listes. Cependant, ce n’est pas important pour le tri-fusion, car les deux listes sont triées avant d’être fusionnées, ce qui annule l’inversion initiale.
Exercice 3
def fusion(l1, l2):
lst = None
while l1 is not None or l2 is not None:
if l1 is not None and (l2 is None or l1.valeur <= l2.valeur):
lst, l1 = Cellule(l1.valeur, lst), l1.suivante
else:
lst, l2 = Cellule(l2.valeur, lst), l2.suivante
# Puis on inverse la liste lst
r = None
while lst is not None:
r, lst = Cellule(lst.valeur, r), lst.suivante
return r
Exercice 4
def deplace(a, b, c, k):
"""Déplace k disques de la tour a vers la tour b, en se servant de la tour c comme intermédiaire"""
if k > 0:
deplace(a, c, b, k - 1)
print("déplace de", a, "vers", b)
deplace(c, b, a, k - 1)
def hanoi(n):
deplace(1, 3, 2, n)
Exercice 5
Pour déplacer $N$ disques, il faut au total $2^N - 1$ déplacements élémentaires. La preuve se fait par récurrence :
* Pour $N=1$, il faut $2^1 - 1 = 1$ déplacement.
* Si l'on suppose qu'il faut $2^{N-1} - 1$ déplacements pour $N-1$ disques, alors pour $N$ disques, on aura :
* $2^{N-1} - 1$ déplacements pour déplacer les $N-1$ premiers disques de la tour de départ à la tour intermédiaire.
* 1 déplacement pour le plus grand disque de la tour de départ à la tour d'arrivée.
* $2^{N-1} - 1$ déplacements pour déplacer les $N-1$ disques de la tour intermédiaire à la tour d'arrivée.
* Total : $(2^{N-1} - 1) + 1 + (2^{N-1} - 1) = 2 \times 2^{N-1} - 1 = 2^N - 1$.
Exercice 6
def hanoi_piles(n):
a = Pile()
for i in range(n, 0, -1):
a.empiler(i)
deplace(a, Pile(), Pile(), n)
def deplace(a, b, c, k):
"""déplace k disques de la pile a vers la pile b, en se servant de la pile c comme intermédiaire"""
if k > 0:
deplace(a, c, b, k - 1)
b.empiler(a.depiler())
deplace(c, b, a, k - 1)
Exercice 7
def rotation_aux(px, x, y, t):
'''on va faire la rotation de l'image située entre les pixels de coordonnées (x,y) et (x+t,y+t)'''
if t == 1:
return
t //= 2
rotation_aux(px, x, y, t)
rotation_aux(px, x + t, y, t)
rotation_aux(px, x, y + t, t)
rotation_aux(px, x + t, y + t, t)
for x1 in range(x, x + t):
for y1 in range(y, y + t):
px[x1, y1 + t]=px[x1, y1]
px[x1 + t, y1 + t]= px[x1, y1 + t]
px[x1 + t, y1]= px[x1 + t, y1 + t]
px[x1, y1] =px[x1 + t, y1]
def rotation(px, taille):
rotation_aux(px, 0, 0, taille)
Exercice 8
voici deux version du programme en Python. Il faudra copier l’une ou l’autre (car les noms de fonctions sont les mêmes dans les deux versions)
#en base 10
def taille(x):
n = 1
while x > 0:
x //= 10
n += 1
return n
def karatsuba(x, y, n):
"""multiplie x et y par la méthode de Karatsuba"""
if n <= 1:
return x * y
n //= 2
a, b = x // 10**n, x % 10**n
c, d = y // 10**n, y % 10**n
ac = karatsuba(a, c, n)
bd = karatsuba(b, d, n)
abcd = karatsuba(a - b, c - d, n)
return (ac * 10 ** (2 * n)) + ((ac + bd - abcd) * 10**n) + bd
def mult(x, y):
n = max(taille(abs(x)), taille(abs(y)))
return karatsuba(x, y, n)
print(mult(2457,6819))
# en base 2
def taille(x):
n = 1
while x > 0:
x //= 2
n += 1
return n
def karatsuba(x, y, n):
"""multiplie x et y par la méthode de Karatsuba"""
if n <= 1:
return x * y
n //= 2
m = 1 << n
a, b = x >> n, x % m
c, d = y >> n, y % m
ac = karatsuba(a, c, n)
bd = karatsuba(b, d, n)
abcd = karatsuba(a - b, c - d, n)
return (ac << (2 * n)) + ((ac + bd - abcd) << n) + bd
def mult(x, y):
n = max(taille(abs(x)), taille(abs(y)))
return karatsuba(x, y, n)
Ping : Terminale NSI 2025-26 – Maths & Informatique
Ping : La méthode « Diviser pour régner » – Maths & Informatique