Exercice 1 : Le Problème de la Coupe de Barres d’Acier (Rod Cutting)
Ce problème, inspiré du livre « Introduction to Algorithms, » vise à maximiser le revenu obtenu en coupant une barre d’acier de longueur n en morceaux plus petits.
Données tarifaires :
| Longueur i (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix pi (€) | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
L’entreprise Sun & Steel peut vendre une barre entière ou la découper pour maximiser son revenu.
Partie I : Analyse et Récursivité Naïve
1) Exploration des possibilités pour n=4 : La barre de 4 m peut être coupée de plusieurs façons. Continuez la liste ci-dessous pour trouver toutes les combinaisons de découpes et déterminez le revenu maximum r4 possible :
- Vente entière (4): 9€
- Découpe en 2 morceaux (2+2): 5+5=10€
- Découpe en 2 morceaux (1+3): 1+8=9€
- Découpe en 3 morceaux (1+1+2): 1+1+5=7€
- … Ajoutez les combinaisons manquantes (par ex. 1+1+1+1, 1+2+1, etc.)
2) Formulation de la Relation de Récurrence : Le revenu maximum rn pour une barre de longueur n peut être calculé en considérant toutes les premières coupes possibles. On coupe la barre de longueur n en un premier morceau de longueur i (vendu au prix pi) et on optimise le revenu sur le morceau restant de longueur n−i (qui rapporte rn−i).La relation de récurrence est donc : rn=max(pi+rn−i) où 1≤i≤n et r0=0 (revenu pour une barre de longueur nulle).Utilisez cette relation pour retrouver la valeur de r4 en utilisant les revenus maximaux déjà calculés : r1=1,r2=5,r3=8.
r4=max(p1+r3, p2+r2, p3+r1, p4+r0)
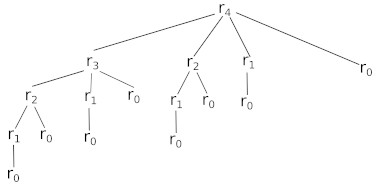
3) Implémentation Récursive (Naïve) : Complétez la fonction récursive ci-dessous, qui implémente directement la relation rn=max1≤i≤n(pi+rn−i).
def revenu_barre(n):
prix = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # Indice 0 inutilisé, prix[1] = p1, etc.
if n == 0:
return … # Cas de base
r = float('-inf') # Initialisation au minimum possible
for i in range(1, n + 1):
# i est la longueur du premier morceau coupé
r = max(r, prix[i] + ...) # Terme récursif à ajouter
return r
4) Application : Utilisez la fonction revenu_barre pour calculer les revenus maximaux r5,r6,r7,r8,r9 et r10.
5) Changement de Tarifs : Le nouveau tableau de prix est proposé dans le tableau proposé plus bas.
Modifiez le tableau prix dans la fonction revenu_barre et recalculez les revenus maximaux rn pour n allant de 5 à 10.
| Longueur i (m) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Prix pi (€) | 1 | 6 | 9 | 11 | 12 | 19 | 20 | 23 | 24 | 26 |
Partie II : Optimisation par Programmation Dynamique
L’approche récursive simple entraîne de nombreux recalculs inutiles (sous-problèmes qui se chevauchent).
Pour une barre de 4 m, l’arbre de calcul montre que r1 est calculé 4 fois et r2 est calculé 2 fois. La programmation dynamique permet d’éviter cette redondance.
- Approche Descendante (Mémorisation) : Écrivez une fonction
revenu_barre_dyn_desc(n)qui utilise la mémorisation (un tableaumem) pour stocker et réutiliser les valeurs de ri déjà calculées, évitant ainsi les appels récursifs redondants.- Indice : La structure sera similaire à
fib_memdu cours. Le tableaumemstocke ri. Avant tout appel récursif, vérifiez simem[n]est déjà calculé.
- Indice : La structure sera similaire à
- Approche Ascendante (Itérative) : Écrivez une fonction
revenu_barre_dyn_asc(n)qui utilise une méthode itérative (boucles) pour calculer ri séquentiellement, de r1 à rn, en stockant les résultats dans un tableau.- Indice : Initialisez un tableau
tabde taille n+1 avec tab[0]=0. Utilisez une boucleforallant de m=1 à n pour calculer tab[m] en utilisant la relation de récurrence et les valeurs déjà présentes dans le tableau.
- Indice : Initialisez un tableau
Exercice 2 : Score Maximal dans une Pyramide de Nombres
Ce problème consiste à trouver le chemin de score maximal en partant du sommet d’une pyramide et en descendant en choisissant, à chaque niveau, l’élément immédiatement à gauche ou à droite.
La pyramide est représentée par une liste de listes. Exemple : ex1 = [[4],[6,2],[3,5,7],[5,1,6,2],[4,7,3,5,2]]
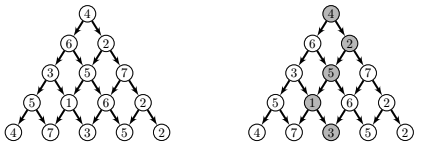
En gris on peut lire un des chemins possibles (qui est loin d’être le plus long) son score sera : 4 + 2 + 5 + 1 + 3 = 15.
Partie I : Représentation et Fonctions de Base
- Représentation : Dessinez la pyramide représentée par la liste de listes
ex2 = [[3],[1,2],[4,5,9],[3,6,2,1]]. - Chemins et Indices : Un chemin est représenté par la liste des indices choisis à chaque niveau. Par exemple, le chemin gris dans
ex1estch1 = [0,1,1,1,2]. Dessinez le cheminch2 = [0,1,2,2]dans la pyramideex2. - Calcul du Score : Calculez le score du chemin
ch2 = [0,1,2,2]dans la pyramideex2. - Fonction de Validation : Écrivez une fonction
est_chemin(ch, p)qui vérifie si une liste d’indiceschest un chemin valide dans la pyramidep. Les règles sont :- Doit commencer par 0 (
ch[0] == 0). - La longueur de
chdoit être égale au nombre de niveaux dep. - Chaque indice consécutif b (au niveau i+1) doit être a ou a+1 par rapport à l’indice précédent a (au niveau i).
- Tests :
est_chemin(ch2, ex2)doit renvoyerTrue.est_chemin([0, 0, 0, 2], ex2)doit renvoyerFalse.
- Doit commencer par 0 (
- Fonction de Score : Écrivez une fonction
score(ch, p)qui prend un chemin valide et la pyramide, et renvoie le score total.- Test :
score(ch1, ex1)doit renvoyer 15.
- Test :
Partie II : Programmation Dynamique pour l’Optimisation
Le problème du chemin maximal présente une structure de sous-problèmes optimaux. Le chemin optimal de la pyramide entière est composé du sommet et du chemin optimal de l’une des deux sous-pyramides adjacentes.

Soit score_max(i,j) le score maximal possible à partir du nombre situé à l’indice j du niveau i.
Les relations sont :
- Cas de base (dernier niveau) : score_max(len(p)−1,j)=p[len(p)−1][j]
- Cas récursif : score_max(i,j)=p[i][j]+max(score_max(i+1,j),score_max(i+1,j+1))
- Implémentation Récursive (Naïve) : Écrivez une fonction
calcule_score_max(p)qui utilise directement la relation de récurrence pour trouver le score maximal score_max(0,0). - Préparation pour la PD : Écrivez une fonction
pyramide_nulle(n)qui crée une structure de pyramide (liste de listes) de n niveaux, remplie de zéros. Cette pyramide servira de tableau de mémorisation. - Approche Ascendante (Programmation Dynamique) : Écrivez une fonction
prog_dyn(p)qui calcule le score maximal en utilisant la programmation dynamique ascendante (du bas vers le haut).- Créez une pyramide de mémorisation s de la même taille que p.
- Commencez par initialiser le dernier niveau de s avec les valeurs du dernier niveau de p.
- Remontez itérativement niveau par niveau (de len(p)−2 jusqu’à 0), en appliquant la formule score_max(i,j).
- Le résultat final sera s[0][0].
- Analyse de Complexité : Déterminez l’ordre de grandeur du coût (complexité en temps) de la fonction
prog_dyn(p)pour une pyramide à n niveaux (sachant que le nombre d’éléments au niveau i est i+1).
Exercice 1 : Analyse de la Récursivité Naïve (Rendu de Monnaie)
Objectif : Identifier l’inefficacité des algorithmes récursifs sans mémorisation.
Énoncé : Soit la fonction récursive rendu_monnaie qui calcule le nombre minimal de pièces pour une somme donnée, sans utiliser la programmation dynamique :
Python
def rendu_monnaie(pieces, s):
"""
Renvoie le nombre minimal de pièces pour faire la somme s
avec le système 'pieces' (approche récursive naïve).
"""
if s == 0:
return 0
r = s # Initialisation au pire cas (1+1+...+1)
for p in pieces:
if p <= s:
r = min(r, 1 + rendu_monnaie(pieces, s - p))
return r
Question : Explicitez (à la main) tous les appels récursifs effectués par la fonction lorsque vous exécutez rendu_monnaie([1, 2], 3). Identifiez clairement les calculs redondants (les sous-problèmes qui sont résolus plusieurs fois).
Exercice 2 : Rendu de Monnaie par Programmation Dynamique (Ascendante)
Objectif : Comprendre le remplissage du tableau de mémorisation dans l’approche ascendante (Bottom-up).
Énoncé : Soit le programme d’approche ascendante (Programmation Dynamique) pour le rendu de monnaie :
Python
def rendu_monnaie(pieces, s):
"""
Renvoie le nombre minimal de pièces pour faire la somme s
avec le système 'pieces' (approche dynamique ascendante).
"""
nb = [0] * (s + 1) # Tableau de mémorisation
for n in range(1, s + 1):
nb[n] = n # Initialisation au pire cas (1+1+...+1)
for p in pieces:
if p <= n:
# Mise à jour: 1 + nb[n - p] est le nombre de pièces si on prend la pièce p
nb[n] = min(nb[n], 1 + nb[n - p])
return nb[s]
Question : Calculez à la main et présentez l’état final du tableau nb lorsque l’on exécute rendu_monnaie([1, 6, 10], 12).
Exercice 3 : Rendu de Monnaie avec Solution Optimale
Objectif : Étendre l’approche dynamique pour tracer et reconstruire la solution (les pièces utilisées).
Énoncé : Modifiez le programme rendu_monnaie de l’Exercice 2 pour qu’il renvoie non seulement le nombre minimal de pièces, mais aussi la liste exacte des pièces qui composent cette solution optimale. Vous pouvez vous inspirer de l’exemple fourni (rendu_monnaie_solution).
Exercice 4 : Suite de Fibonacci par Programmation Dynamique
Objectif : Appliquer la PD à la suite de Fibonacci en utilisant l’approche ascendante (itérative).
Énoncé : La suite de Fibonacci est définie par F0=0,F1=1 et Fn=Fn−1+Fn−2 pour n≥2. Écrivez une fonction fibonacci(n) qui calcule la valeur de Fn en utilisant la programmation dynamique (approche itérative, sans récursion).
voici un programme d’alignement de séquences fondamental sur lequel vont venir s’appuyer les exercices à suivre
def aligne(s1, s2):
"""le score du meilleur alignement de s1 et s2"""
n1, n2 = len(s1), len(s2)
sc = [[0] * (n2 + 1) for _ in range(n1 + 1)]
# première ligne et première colonne
for i in range(1, n1 + 1):
sc[i][0] = -i
for j in range(1, n2 + 1):
sc[0][j] = -j
# le reste
for i in range(1, n1 + 1):
for j in range(1, n2 + 1):
s = max(-1 + sc[i - 1][j], -1 + sc[i][j - 1])
if s1[i - 1] == s2[j - 1]:
sc[i][j] = max(s, 1 + sc[i - 1][j - 1])
else:
sc[i][j] = max(s, -1 + sc[i - 1][j - 1])
return sc[n1][n2]
Exercice 5 : Calcul du Tableau d’Alignement (Sequence Alignment)
Objectif : Appliquer manuellement la formule de récurrence du Programme 48 sur un petit exemple.
Énoncé : Le programme d’Alignement de Séquences (voir avant l’exercice 5) utilise la Programmation Dynamique pour calculer le score maximal d’alignement entre deux chaînes. Les règles de score utilisées par ce programme sont :
- Match : +1
- Mismatch : −1
- Gap (-) : −1
Question : Calculez à la main le tableau des scores d’alignement (sc) pour les deux mots « CHAT » et « CAT ». Quel est le score maximal final ?
Exercice 6 : Alignement de Séquences Identiques (Mismatchs)
Objectif : Déterminer la structure du tableau lorsque tous les alignements sont des mismatchs ou des gaps.
Énoncé : En utilisant les règles de score du programme d’Alignement de Séquences (voir avant l’exercice 5) (+1 pour match, -1 pour mismatch/gap), quel est le score maximal d’alignement des mots s1= »AAAAAAAAAA » et s2= »BBBBBBBBBB » (10 caractères chacun) ? Décrivez la forme du tableau calculé.
Exercice 7 : Affichage Formatté de la Table de Scores
Objectif : Créer une fonction utilitaire pour visualiser le tableau de Programmation Dynamique.
Énoncé : Écrivez une fonction affiche(s1, s2, sc) qui prend les deux séquences (s1, s2) et le tableau des scores (sc) calculé par le Programme 48, et affiche la table sous un format lisible et aligné.
Exercice 8 : Alignement avec Solution (Reconstruction)
Objectif : Modifier le programme d’alignement pour reconstruire la séquence d’opérations menant au score optimal.
Énoncé : Modifiez Le programme d’Alignement de Séquences (voir avant l’exercice 5) pour qu’il renvoie également la solution optimale sous la forme d’un couple de chaînes alignées (avec le caractère - pour les gaps).
Exercice 9 : Alignement avec Matrice de Similarités et Coût de Gap
Objectif : Généraliser le Programme 48 pour utiliser une matrice de similarités personnalisée et un coût de gap variable.
Énoncé : Dans les alignements biologiques (ADN), les scores ne sont pas fixes. Nous utilisons :
- Une matrice de similarités (
sim) pour le score d’alignement entre deux caractères spécifiques. - Une variable globale
gappour le coût de création d’un gap (-).
Question : Indiquez comment représenter la matrice de similarités en Python et modifiez le programme d’Alignement de Séquences (voir avant l’exercice 5) pour utiliser ces variables (sim et gap).
Exercice 10 : Nombre de Chemins sur une Grille
Objectif : Résoudre un problème de dénombrement par Programmation Dynamique.
Énoncé : Écrivez une fonction chemins(n, m) qui calcule le nombre de chemins possibles sur une grille de taille n×m (partant du coin supérieur gauche 0,0 jusqu’au coin inférieur droit n,m), en se déplaçant uniquement vers la droite ou vers le bas.