technique pour améliorer les Algorithmes Récursifs
La programmation dynamique est une puissante technique algorithmique qui transforme des solutions récursives « naïves » mais correctes en des solutions beaucoup plus efficaces en évitant les recalculs inutiles. Nous allons explorer cette méthode à travers un exemple classique, la suite de Fibonacci, et ensuite l’appliquer à un problème d’optimisation : le problème du sac à dos (Knapsack Problem).
1) La Suite de Fibonacci et le Recalcul Inutile
L’Approche Récursive Simple
La suite de Fibonacci (Fn) est définie par F0=0, F1=1, et Fn=Fn−1+Fn−2 pour n≥2. Une implémentation récursive directe en Python est la suivante :
Python
def fib_recursif(n):
if n < 2:
return n
else:
return fib_recursif(n-1) + fib_recursif(n-2)
Pour calculer F6, l’exécution de ce code crée une structure arborescente d’appels. Si l’on déploie cet arbre pour F6, on constate une forte redondance des calculs.
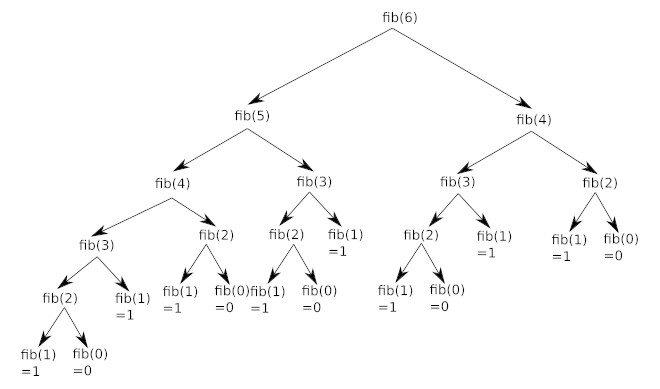
Par exemple, le calcul de F4 est effectué deux fois, celui de F3 est effectué trois fois, etc. Cette duplication des efforts entraîne une complexité temporelle qui augmente de manière exponentielle (O(2n)), rendant cette approche impraticable pour de grandes valeurs de n.
En observant attentivement le schéma ci-dessus, vous avez remarqué que de nombreux calculs sont inutiles, car effectués 2 fois : par exemple, on retrouve le calcul de fib(4) à 2 endroits (en haut à droite et un peu plus bas à gauche) :
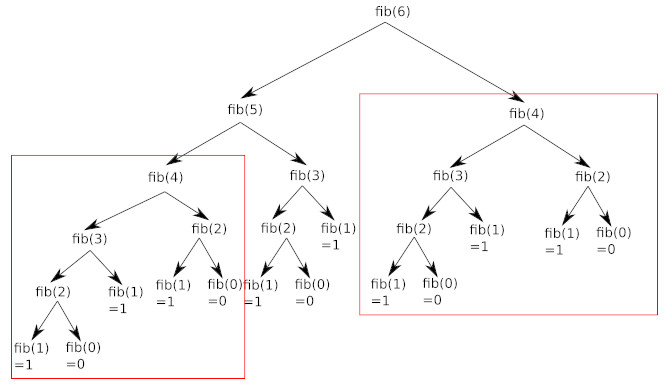
L’Optimisation par Mémorisation (Approche Descendante)
L’idée fondamentale est d’éviter de recalculer un résultat une fois qu’il a été obtenu. Nous allons « mémoriser » la solution de chaque sous-problème (Fk) dans un tableau ou un dictionnaire au fur et à mesure que nous le calculons.
Python
def fib_mem(n):
# Initialise un tableau pour stocker les résultats.
# Tous les résultats sont initialisés à 0 (ou une valeur "jamais calculée").
memo = [0] * (n + 1)
def f_mem(k):
if k == 0 or k == 1:
# Cas de base : on mémorise et retourne la valeur
memo[k] = k
return k
# Vérification 1 : Si le résultat est déjà mémorisé, on le retourne directement.
elif memo[k] > 0: # > 0 car F0=0 et on suppose n>0 pour les autres
return memo[k]
# Calcul : Si le résultat n'est pas mémorisé, on le calcule
else:
memo[k] = f_mem(k - 1) + f_mem(k - 2)
return memo[k]
return f_mem(n)
Principe de la Mémorisation :
- Si la valeur de Fk a déjà été calculée (si elle est dans le tableau
memo), on l’utilise sans faire de calcul supplémentaire. - Si la valeur de Fk n’a jamais été calculée, elle est calculée une unique fois, puis stockée dans le tableau
memopour une utilisation ultérieure.
Cette technique, appelée mémorisation (ou memoization), résout le problème Fk une seule fois, transformant la complexité exponentielle en une complexité beaucoup plus efficace, linéaire (O(n)). On parle ici de programmation dynamique descendante (top-down), car nous partons du problème principal (Fn) et le décomposons jusqu’aux cas de base (F0,F1).
2) La Programmation Dynamique
a) Introduction et Concepts Fondamentaux
La Programmation Dynamique (PD) est une méthode algorithmique pour résoudre des problèmes complexes en les décomposant en sous-problèmes plus simples. Inventée par Richard Bellman dans les années 1950, le terme « programmation » est à prendre dans le sens de planification ou d’ordonnancement d’un processus, et non de codage.
La PD s’applique efficacement aux problèmes qui présentent deux caractéristiques principales :
- Sous-problèmes Optimaux : Une solution optimale au problème principal doit être construite à partir de solutions optimales à ses sous-problèmes (principe de Bellman).
- Sous-problèmes Réciproques (Overlapping Subproblems) : Les sous-problèmes se recoupent, c’est-à-dire que le même sous-problème est rencontré et doit être résolu plusieurs fois.
La PD résout chaque sous-problème une seule fois et mémorise sa réponse, évitant ainsi le coût du recalcul.
b) Approche Ascendante (Bottom-Up)
L’approche ascendante (ou bottom-up) est la deuxième facette de la programmation dynamique. Au lieu d’utiliser la récursivité et la mémorisation (descendante), elle utilise une approche itérative (boucles) pour construire la solution des plus petits sous-problèmes vers le problème principal.
Fibonacci avec l’Approche Ascendante
Pour Fibonacci, l’idée est de remplir le tableau des résultats en partant de F0 et F1 et en montant jusqu’à Fn.
Python
def fib_asc(n):
if n < 2:
return n
# Crée un tableau pour stocker F0, F1, ..., Fn
tab = [0] * (n + 1)
tab[1] = 1 # Initialise F1
# Calcule F2, F3, ..., Fn de manière itérative
for i in range(2, n + 1):
tab[i] = tab[i - 1] + tab[i - 2]
return tab[n]
Ce programme est très simple. On construit Fi à partir de Fi−1 et Fi−2 qui ont déjà été calculés et stockés dans le tableau tab. Chaque Fi est calculé une seule fois.
3) Application à l’Optimisation : Le Problème du Sac à Dos (Knapsack Problem 0/1)
Le problème du sac à dos (0/1) est un problème d’optimisation classique : Étant donné un sac à dos de capacité maximale W et une liste d’objets, chacun avec un poids pi et une valeur vi, déterminer quels objets inclure dans le sac afin de maximiser la valeur totale sans dépasser la capacité W.
Ce problème ne peut pas être résolu de manière gloutonne (greedy) de manière fiable (par exemple, prendre toujours l’objet de plus grande valeur ou le meilleur rapport valeur/poids ne garantit pas la solution optimale globale).
Formulation Récursive et Sous-problèmes
Pour déterminer la valeur maximale que l’on peut obtenir avec une capacité w et les i premiers objets, nous avons deux choix pour l’objet i :
- On inclut l’objet i : La valeur totale sera vi plus la valeur maximale obtenue avec la capacité restante w−pi et les i−1 premiers objets. (Possible seulement si pi≤w).
- On n’inclut pas l’objet i : La valeur totale sera la valeur maximale obtenue avec la capacité w et les i−1 premiers objets.
La relation de récurrence (pour un objet i de poids pi et valeur vi, et une capacité w ) est :
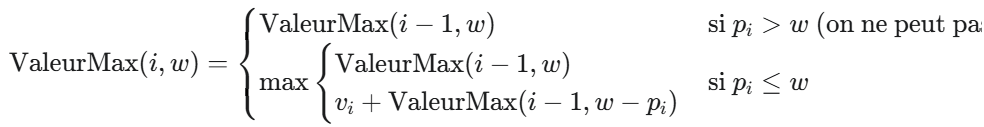
Résolution par Programmation Dynamique Ascendante
Nous allons utiliser l’approche ascendante pour construire un tableau bidimensionnel DP, où DP[i][w] représente la valeur maximale que l’on peut obtenir en utilisant les i premiers objets pour une capacité de sac à dos w.
Exemple : Capacité W=5. Objets : O1(p=2,v=3), O2(p=3,v=4), O3(p=4,v=5).
| Objets / Capacité (w) | 0 | 1 | 2 | 3 | 4 | 5 |
| Aucun objet (i=0) | 0 | 0 | 0 | 0 | 0 | 0 |
| O1 (p=2, v=3) | 0 | 0 | 3 | 3 | 3 | 3 |
| O2 (p=3, v=4) | 0 | 0 | 3 | 4 | 4 | 7 |
| O3 (p=4, v=5) | 0 | 0 | 3 | 4 | 5 | 7 |
Exporter vers Sheets
Analyse du tableau :
- DP[1][2]: Pour w=2 et seul l’objet O1 disponible. Puisque p1=2≤2, DP[1][2]=max(DP[0][2],v1+DP[0][2−2])=max(0,3+0)=3.
- DP[2][5]: Pour w=5 et les objets O1,O2 disponibles. Puisque p2=3≤5, DP[2][5]=max(DP[1][5],v2+DP[1][5−3])=max(3,4+DP[1][2]). DP[1][2]=3. Donc max(3,4+3)=7. (On prend O2 et on utilise la meilleure valeur pour la capacité restante de 2 avec l’objet O1).
La solution optimale est donnée par DP[N][W] (ici DP[3][5]=7). Le problème est résolu avec une complexité en temps de O(N×W), où N est le nombre d’objets et W la capacité maximale, bien plus efficace qu’une approche par force brute (tester toutes les combinaisons).
Coût vs Bénéfice
Comme pour Fibonacci, la programmation dynamique permet un gain spectaculaire en complexité temporelle (le temps d’exécution). Cependant, elle nécessite l’utilisation d’une structure de données (le tableau memo ou le tableau DP) pour stocker les résultats des sous-problèmes.
Conclusion : La programmation dynamique échange de l’efficacité en temps contre une augmentation de l’utilisation de la mémoire (complexité spatiale).
L’Alignement de Séquences : Le Détective de l’ADN 🕵️♀️
1. Le Problème : Comparer l’ADN (ou des Mots !)
Imaginez que vous êtes un détective et que vous avez deux longues chaînes de caractères (comme des brins d’ADN, ou simplement deux mots) que vous devez comparer pour voir à quel point elles sont similaires.
C’est le problème de l’Alignement de Séquences : comment mettre en face les caractères de deux chaînes pour maximiser les correspondances.
La Règle du Jeu : L’Alignement
Pour comparer deux mots (par exemple, « GENOME » et « ENORME »), nous allons les écrire l’un sous l’autre. Nous pouvons insérer des trous (représentés par un tiret, -) dans l’une ou l’autre chaîne.
- Contrainte essentielle : L’ordre des lettres ne doit jamais changer !
- Contrainte essentielle : On n’aligne jamais deux trous ensemble (
--est interdit).
| Alignement 1 (Bon) | Alignement 2 (Mauvais) |
| G E N O – M E | G – E N O M E |
| – E N O R M E | E – N O R M E |
Exporter vers Sheets
Comment Compter les Points (Le Score)
Pour trouver le « meilleur » alignement, on utilise un système de points simple :
| Action | Score |
| Match (caractères identiques) | +1 point (C’est super !) |
| Mismatch (caractères différents) | -1 point (C’est pas bon) |
Gap (aligner un caractère avec un trou -) | -1 point (C’est pas bon) |
Exporter vers Sheets
Exemple d’évaluation (GENO-ME vs -ENORME) :
| Aligné | G vs – | E vs E | N vs N | O vs O | – vs R | M vs M | E vs E |
| Score | −1 (Gap) | +1 (Match) | +1 (Match) | +1 (Match) | −1 (Gap) | +1 (Match) | +1 (Match) |
Exporter vers Sheets
Score Total : (−1)+(+1)+(+1)+(+1)+(−1)+(+1)+(+1)=3
Le but de l’algorithme est de trouver l’alignement qui donne le score maximal possible.
2. L’Approche « Bête et Méchante » (Récursivité Naïve)
Comment un ordinateur chercherait-il la meilleure solution ?
Il pourrait essayer de le faire de manière récursive, c’est-à-dire en se ramenant à un problème plus petit à chaque étape.
La Décomposition Récursive
Pour trouver le meilleur score entre deux mots M1 et M2, il suffit de regarder leurs derniers caractères (c1 et c2). Il y a toujours trois choix possibles pour l’alignement final :
| Choix | Description de l’action finale | Score pour cette action | Le nouveau problème à résoudre |
| 1. Diagonale | Aligner c1 avec c2 | +1 (si c1=c2) ou −1 (si c1=c2) | Trouver le meilleur score pour M1 sans c1 et M2 sans c2 |
| 2. Verticale | Aligner c1 avec un trou - | −1 (Gap) | Trouver le meilleur score pour M1 sans c1 et M2 (entier) |
| 3. Horizontale | Aligner c2 avec un trou - | −1 (Gap) | Trouver le meilleur score pour M1 (entier) et M2 sans c2 |
Exporter vers Sheets
Le Score Maximal pour M1 et M2 est simplement le maximum des scores obtenus par ces trois choix. On répète ensuite l’opération (récursion) sur les mots plus courts.
Le Problème des Recalculs (Pourquoi ça explose 💣)
Si on utilise cette approche, l’ordinateur va vite se retrouver à faire la même chose encore et encore.
Exemple : Pour aligner « GENOME » et « ENORME » :
- Le Choix 1 vous demande d’aligner « GENOM » et « ENORM ».
- Le Choix 2 vous demande d’aligner « GENOM » et « ENORME ».
- Le Choix 3 vous demande d’aligner « GENOME » et « ENORM ».
Regardez le problème « GENOM » et « ENORM » : Il est calculé comme sous-problème dans les trois cas ! Ce problème est dit un sous-problème qui se chevauche.
Pour des mots de 20 lettres, ce phénomène de duplication se répète des milliards de fois, et le temps de calcul devient exponentiel (beaucoup trop lent !).
3. La Solution Intelligente : La Programmation Dynamique 🧠
Comme pour le problème du Rendu de Monnaie, nous allons utiliser la Programmation Dynamique (PD) pour éviter de recalculer les mêmes sous-problèmes. L’idée est de mémoriser chaque résultat.
Le Tableau de Scores (La « Carte »)
Au lieu de faire des appels récursifs et de tout oublier, nous allons construire un grand tableau à deux dimensions, appelé le tableau de scores (sc).
- Si le premier mot (s1) a N lettres et le deuxième mot (s2) a M lettres, le tableau aura une taille de (N+1)×(M+1).
- La case
sc[i][j]va stocker le score maximal obtenu en alignant les i premières lettres de s1 avec les j premières lettres de s2.
| sc | – | s2[0] | s2[1] | … | s2[M−1] |
| – | sc[0][0] | sc[0][1] | sc[0][2] | … | sc[0][M] |
| s1[0] | sc[1][0] | sc[1][1] | sc[1][2] | … | sc[1][M] |
| s1[1] | sc[2][0] | sc[2][1] | … | … | … |
| … | … | … | … | … | … |
| s1[N−1] | sc[N][0] | sc[N][1] | … | … | sc[N][M] |
Exporter vers Sheets
Le résultat que nous cherchons est toujours la case en bas à droite : sc[N][M].
L’Initialisation des Bords (Les Cas Simples)
On commence par remplir la première ligne et la première colonne (les cas où l’on aligne un mot avec un mot vide).
- sc[0][0]=0 : Aligner deux mots vides donne un score de 0.
- sc[i][0]=−i : Pour aligner les i premières lettres de s1 avec un mot vide, nous devons faire i gaps (trous). Le coût est donc i×(−1)=−i.
- sc[0][j]=−j : De même, aligner s2 avec un mot vide coûte −j.
Le Remplissage des Cases (Le Cœur du Calcul)
Pour remplir une case sc[i][j], nous utilisons la logique récursive des trois choix, mais au lieu d’appeler la fonction, nous regardons simplement les trois cases voisines qui ont déjà été calculées :
- Voisin du Dessus (
sc[i-1][j]) → Correspond au Choix 2 (Gap dans s2). - Voisin de Gauche (
sc[i][j-1]) → Correspond au Choix 3 (Gap dans s1). - Voisin en Diagonale (
sc[i-1][j-1]) → Correspond au Choix 1 (Alignement des deux derniers caractères s1[i−1] et s2[j−1]).
La formule de calcul (la relation de récurrence) devient :
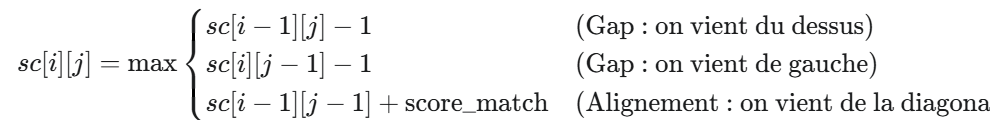
Où score_match=+1 si s1[i−1]=s2[j−1], et −1 sinon.
L’Efficacité : Un Gain Incroyable 🚀
Grâce à cette méthode :
- Chaque case du tableau n’est calculée qu’une seule fois !
- Pour des mots de longueur N et M, le temps de calcul est proportionnel à la taille du tableau, soit N×M.
C’est une amélioration massive :
- Récursivité naïve : Temps exponentiel (O(2max(N,M))). Impraticable au-delà de 20 lettres.
- Programmation Dynamique : Temps polynomial (O(N×M)). C’est presque instantané même pour des séquences de milliers de caractères !
Ce tableau ne sert pas seulement à trouver le score maximal ; en remontant de la case finale à la case initiale en suivant les flèches du meilleur score à chaque fois, on peut reconstruire l’alignement optimal lui-même (comme vous le verrez dans certains exercices).