Graphes (partie 1)

Activité : « Qui suit qui ? »

1. La mise en situation

Dessiner sur votre feuille 5 prénoms (Alice, Bob, Charles, Driss, Elsa) éparpillés de manière aléatoire. Voici leurs relations sur Instagram :

Alice suit Bob et Elsa.

Bob suit Alice.

Charles suit Alice et Driss.

Driss ne suit personne.

Elsa suit Bob et Charles.

Consigne : Représenter ces relations par des flèches sur leur cahier.

2. Pourquoi pas une liste ?

Nous avons vu les listes chaînées où chaque nœud a un seul suivant. Pourquoi est-ce que notre classe Cellule habituelle ne suffit pas pour modéliser cette situation ? »

3. Formalisation

Introduisez le vocabulaire de base en utilisant le dessin de correction :

Les personnes sont des ……………………………………….

Les flèches sont des ……………………………………………

L’ensemble s’appelle …………………………………………..

4. Comment coder ça ?

Si on devait créer une classe Sommet, à quoi ressemblerait son constructeur pour qu’on puisse retrouver ses abonnés ? »

class Sommet:
    def __init__(self, nom):
        ………………………………………….
        ………………………………………….

# Exemple de création
a = Sommet("Alice")
b = Sommet("Bob")
a.voisins.append(b) # Alice suit Bob

Exercice de clôture : Le Réseau des Développeurs

On considère le mini-graphe suivant représentant trois serveurs informatiques connectés :

Le serveur A est connecté au serveur B.

Le serveur B est connecté au serveur C.

Le serveur C est connecté au serveur A (c’est une boucle).

1. En utilisant la classe Sommet définie précédemment, écrivez les instructions Python permettant de créer ces trois serveurs et d’établir leurs connexions.

Si on exécute l’instruction print(a.voisins[0].voisins[0].nom), qu’est-ce qui va s’afficher à l’écran ?

Définition

Un graphe est un objet mathématique très simple avec lequel on peut faire des choses extrêmement compliquées. Il est constitué de sommets (ou nœuds) reliés par des arêtes (ou liens). Si les arêtes sont fléchées, on parle de graphe orienté sinon on parle de graphe non-orienté. Dans un graphe orienté, on appelle parents d’un nœud, les nœuds qui pointent vers lui. On appelle fils d’un nœud, les nœuds vers lesquels il pointe.

Un graphe peut représenter un réseau social, des liens d’amitié, un réseau routier.

1) Pour le graphe ci-dessous, dire s’il est orienté ou non, donner le nombre de sommets et le nombre d’arêtes.

C’est un graphe orienté (il y a des flèches). Il a 6 sommets et 8 arêtes.

2) Pour le graphe ci-dessous, dire s’il est orienté ou non, donner le nombre de sommets et le nombre d’arêtes.

C’est un graphe non-orienté (il n’y a pas de flèches). Il a 5 sommets et 6 arêtes.

On utilisera parfois des graphes pondérés pour représenter par exemple des distances sur une carte. Dans un tel graphe, les arêtes sont associées à un poids :

Propriétés

Les propriété les plus communes pour parler d’un graphe sont les suivantes :

• une chaîne (ou chemin) est une suite d’arêtes consécutives ;
• la longueur d’une chaîne est le nombre d’arêtes qui la compose ;
• la distance entre deux sommets est la longueur de la chaîne la plus courte entre ces deux sommets ;
• un cycle est une chaîne fermée composée d’arêtes distinctes. C’est à dire qui commence et termine par le même sommet et qui n’empreinte pas deux fois la même arête.

3) Pour le graphe ci-dessous, trouvez deux cycles. Donnez également la distance entre A et D.

Voici les trois cycles possibles : DCBD, DCEBD et CEBC. La distance entre A et B est 2.

Représentation

Nous avons utilisé intuituvement une représentation visuelle d’un graphe. Mais nous aurions pû utiliser une description textuelle d’un graphe. Par exemple pour celui de la question 2 :

• A est relié à E ;
• B est relié à C, D et E ;
• C est relié à B, D et E ;
• D est relié à C et B ;
• E est relié à A, B et C.

4) Dessinez le graphe correspondant à la description ci-dessous :KevinMattéoTomEmmaClaireDavid

• Tom est ami avec Emma, Claire et Mattéo ;
• Claire est amie avec Tom, Emma et David ;
• Mattéo est ami avec Tom et Kevin ;
• Emma est amie avec Tom et Claire ;
• David est ami avec Claire ;
• Kevin est ami avec Mattéo.

5) Dessinez le graphe correspondant à la description ci-dessous :

• A est à 12 km de B ;
• B est à 12 km de A, 9 km de C et 25 km de D ;
• C est à 9 km de B ;
• D est à 25 km de B et 6 km de E ;
• E est à 6 km de D.

Implémentations 1

On parle d’implémentation lorsqu’il s’agit de « représenter » un graphe dans un système informatique. Même si nous ne verrons pas directement comment on implémente un graphe en Python nous allons parler des deux principales implémentations d’un graphe.

Matrice d’adjacence

Une matrice n’est qu’un tableau à double entrée :

Nous avons ci-dessus une matrice à 3 lignes et 4 colonnes. En mathématiques on utilise les matrices pour effectuer des calculs, nous les utiliserons ici simplement comme des tableaux à deux dimensions.

Une matrice d’adjacence est une matrice carrée (même nombre de lignes que de colonnes) où chaque ligne et chaque colonne représentent un sommet. Pour un graphe non-orienté on mettra un « 1 » sur la case [i][j] s’il y a une arête entre le sommet i et le sommet j, et un « 0 » sinon. Pour un graphe orienté on mettra un « 1 » sur la case [i][j] s’il y a une arête du sommet i vers le sommet j, et un « 0 » sinon. Pour un graphe pondéré on mettra sur la case [i][j] le poids du lien entre le sommet i et le sommet j.

6) Donnez la matrice d’adjacence du graphe ci-dessous.

7) Donnez la matrice d’adjacence du graphe ci-dessous.

8) Donnez la matrice d’adjacence du graphe ci-dessous.

Listes d’adjacence

Pour un graphe non orienté, une liste d’adjacence associe à chaque sommet la liste de ses voisins. Par exemple, pour le graphe ci-dessous

La liste d’adjacence serait :

• A → [B, C, E] ;
• B → [A] ;
• C → [A, D] ;
• D → [C, E] ;
• E → [A, D].

Pour un graphe orienté, une liste d’adjacence associe à chaque sommet la liste de ses successeurs. C’est à dire les sommets vers lesquels il pointe. Il est également possible de faire une liste d’adjacence des prédécesseurs, ou même les deux pour des raisons de symétrie.

9) Donnez la liste d’adjacence du graphe ci-dessous.

10) Donnez la liste d’adjacence des successeurs du graphe ci-dessous.

Choix d’implémentation

On utilisera une matrice d’adjacence dans le cas d’un graphe avec beaucoup de liens (on parle de graphe dense) et une liste d’adjacence dans le cas contraire. Cela permettra de gagner de la mémoire. Le choix peut aussi dépendre de l’utilité du graphe. En fonction de l’algorithme utilisé, on pourra préférer une implémentation à l’autre.

Implémentations 2

Nous avons vu dans ci-dessus, deux façons de représenter un graphe : par matrice d’adjacence ou par liste d’adjacence. Nous allons utiliser ces deux implémentations ici.

Matrice d’adjacence

Nous utiliserons le même graphe que le précédent :

1) Créez en Python la matrice d’adjacence de ce graphe.

2) (Dificile) Proposez une fonction matrice_largeur permettant de parcourir en largeur ce graphe. On utilisera une liste pour enregistrer les nœuds visités.

3) (Plus dificile) Proposez une fonction matrice_profondeur permettant de parcourir en profondeur ce graphe.

Liste d’adjacence

Nous utiliserons ici le même graphe que précédement.

4) Créez en Python les listes d’adjacence de ce graphe. (On utilisera un tableau à deux dimensions)

5) (Dificile) Proposez une fonction listes_largeur permettant de parcourir en largeur ce graphe. On utilisera une liste pour enregistrer les nœuds visités.

6) (Plus difficile) Proposez une fonction listes_profondeur permettant de parcourir en profondeur ce graphe.

programmes de référence

programme 1 : Graphe représenté par une matrice d’adjacence

class Graphe:
    """un graphe représenté par une matrice d’adjacence,
    où les sommets sont les entiers 0,1,...,n-1"""

    def __init__(self, n):
        self.n = n
        self.adj = [[False] * n for _ in range(n)]

    def ajouter_arc(self, s1, s2):
        self.adj[s1][s2] = True

    def arc(self, s1, s2):
        return self.adj[s1][s2]

    def voisins(self, s):
        v = []
        for i in range(self.n):
            if self.adj[s][i]:
                v.append(i)
        return v

programme 2 : Graphe représenté par un dictionnaire d’adjacence

class Graphe:
    """un graphe comme un dictionnaire d’adjacence"""

    def __init__(self):
        self.adj = {}

    def ajouter_sommet(self, s):
        if s not in self.adj:
            self.adj[s] = set()

    def ajouter_arc(self, s1, s2):
        self.ajouter_sommet(s1)
        self.ajouter_sommet(s2)
        self.adj[s1].add(s2)

    def arc(self, s1, s2):
        return s2 in self.adj[s1]

    def sommets(self):
        return list(self.adj)

    def voisins(self, s):
        return self.adj[s]

programme 3 : Coloriage glouton d’un graphe

def mex(voisins, couleur):
    """la plus petite couleur non utilisée par les voisins"""
    n = len(voisins)
    dispo = [True] * (n + 1)
    for v in voisins:
        if v in couleur and couleur[v] <= n:
            dispo[couleur[v]] = False
    for c in range(n + 1):
        if dispo[c]:
            return c

assert False # on n’arrivera jamais ici

def coloriage(g):
    """colorie graphe g avec un algorithme glouton"""
    couleur = {}
    n = 0
    for s in g.sommets():
        c = mex(g.voisins(s), couleur)
        couleur[s] = c
        n = max(n, c + 1)
    return couleur, n

Exercices

Exercice 1

Dessiner tous les graphes non orientés ayant exactement trois sommets.

Exercice 2

Combien y a-t-il de graphes orientés ayant exactement trois sommets ? On ne demande pas de les dessiner tous, mais seulement de les dénombrer.

Exercice 3

Ajouter à la classe Graphe du programme 1 (matrice d’adjacence) une méthode afficher pour afficher le graphe sous la forme suivante
0 -> 1 3
1 -> 2 3
2 -> 3
3 -> 1
c’est-à-dire une ligne par sommet, avec pour chacun la liste de ses voisins.

Exercice 4

Ajouter à la classe Graphe du programme 2 (dictionnaire d’adjacence) une méthode afficher pour afficher le graphe sous la forme suivante
0 {1, 3}
1 {2, 3}
3 {1}
2 {3}
c’est-à-dire une ligne par sommet, avec pour chacun l’ensemble de ses voisins.
L’ordre des sommets n’est pas important. L’ensemble des voisins peut être affiché directement avec print.

Exercice 5

Ajouter à la classe Graphe du programme 2 une méthode
nb_sommets() qui donne le nombre de sommets du graphe.

Exercice 6

Ajouter à la classe Graphe du programme 1 une méthode degre(s) qui donne le nombre d’arcs issus du sommet s. On appelle cela le degré du sommet s.

Exercice 7

En utilisant l’exercice précédent, ajouter à la classe Graphe du programme 36 une méthode nb_arcs() qui donne le nombre total d’arcs du graphe.

Exercice 8

Ajouter à la classe Graphe du programme 2 une méthode degre(s) qui donne le nombre d’arcs issus du sommet s. On appelle cela le degré du sommet s.

Exercice 9

En utilisant l’exercice précédent, ajouter à la classe Graphe du programme 2 une méthode nb_arcs() qui donne le nombre total d’arcs du graphe.

Exercice 10

Ajouter aux classes Graphe des programmes 1 et 2 une méthode supprimer_arc(s1, s2) pour supprimer l’arc entre les sommets s1 et s2. S’il n’y a pas d’arc entre ces sommets, la méthode n’a aucun effet. On supprime un élément d’un ensemble avec sa méthode remove.

Exercice 11

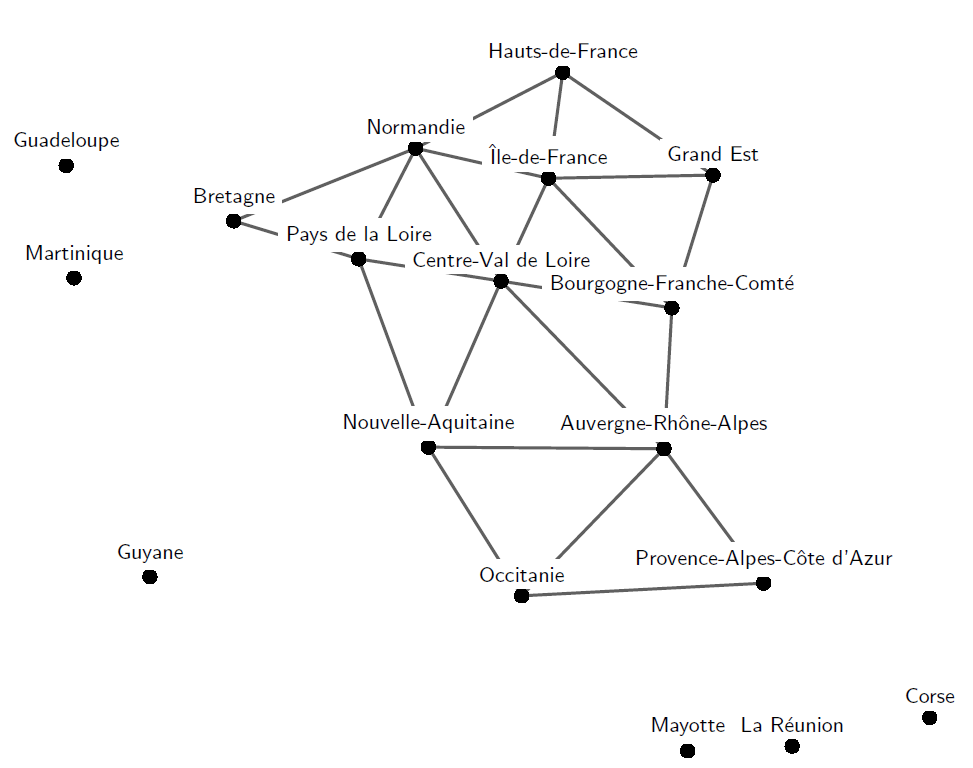
Donner une coloration du graphe des régions ci-dessous qui n’utilise que quatre couleurs.

Corrections

Exercice 1

Il y en a 8 au total

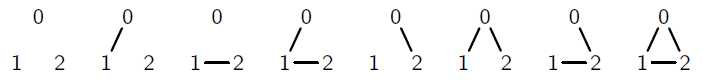
Exercice 2

Il y a six arcs possibles (0 → 1, 1 → 0, 1 → 2, 2 → 1, 2 → 0, 0 → 2), chacun pouvant être présent ou absent, soit 26 = 64
possibilités au total.

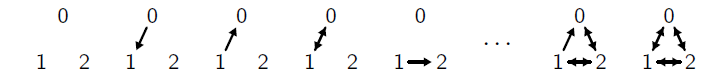
Exercice 3

def afficher(self):
     for s in range(self.n):
     print(s, "->", end="")
     for v in range(self.n):
          if self.adj[s][v]:
               print("", v, end="")
     print()

Exercice 4

On fait un cas particulier pour l’ensemble vide, histoire qu’il ne soit pas affiché comme set() mais comme {}.

def afficher(self):
     for s in self.adj:
          if len(self.adj[s]) == 0:
               print(s, "{}")
          else:
               print(s, self.adj[s])

Exercice 5

Le nombre de sommets est égal au nombre d’entrées dans le dictionnaire :

def nb_sommets(self):
     return len(self.adj)

Exercice 6

Le code est très semblable à celui de la méthode voisins :

def degre(self, s):
     d = 0
     for i in range(self.n):
          if self.adj[s][i]:
               d += 1
     return d

Exercice 7

Il suffit de faire la somme de tous les degrés.

def nb_arcs(self):
     n = 0
     for s in range(self.n):
          n += self.degre(s)
     return n

Exercice 8

C’est exactement le cardinal de l’ensemble adj[s] :

def degre(self, s):
     return len(self.adj[s])

Exercice 9

Comme dans l’exercice 7, on fait la somme de tous les degrés.

def nb_arcs(self):
     n = 0
     for s in self.adj:
          n += self.degre(s)
     return n

Exercice 10

Pour la matrice d’adjacence, on affecte le booléen False dans la matrice :

def supprimer_arc(self, s1, s2):
     self.adj[s1][s2] = False

Pour le dictionnaire d’adjacence, on supprime s2 de l’ensemble des voisins de s1, si l’arc existe :

def supprimer_arc(self, s1, s2):
     if self.arc(s1, s2):
          self.adj[s1].remove(s2)

Exercice 11

Auvergne-Rhône-Alpes 0
Bourgogne-Franche-Comté 1
Bretagne 1
Centre-Val de Loire 2
Corse 0
Grand Est 0
Hauts-de-France 1
Île-de-France 3
Normandie 0
Nouvelle-Aquitaine 1
Occitanie 2
Pays de la Loire 3
Provence-Alpes-Côte dAzur 1
Guadeloupe 0
Martinique 0
Guyane 0
La Réunion 0
Mayotte 0