Comme pour les arbres, il existe différentes façons de parcourir un graphe. On peut le parcourir en largeur ou en profondeur. Le parcours d’un graphe consiste à visiter tous ses nœuds.
Parcours en largeur
Nous allons utiliser des nœuds avec un attribut « visite » à « Faux » par défaut et qui sera mis à « Vrai » lorsqu’il aura été visité. Des nœuds sont dit adjacents ou voisins s’ils sont réliés par une arrête. Voici donc un algorithme du parcours en largeur :
VARIABLES
f : file
nœud : nœud de départ (origine)
x : nœud actuellement visité
y : nœud
DEBUT
nœud.visite = Vrai
f.enfile(nœud)
tant que f est non vide:
x = f.defile()
afficher x
pour chaque y adjacent à x:
si y.visite est Faux:
y.visite = Vrai
f.enfile(y)
FIN
1) Appliquez cet algorithme au graphe ci-dessous en partant de A. On notera sur une même ligne le nœud actuellement visité et le contenu de la file f. Dans le cas de plusieurs voisins, on les ajoutera dans l’ordre alphabétique.

2) Faire un tableau des distances entre A et les autres nœuds.
3) Qui a-t-il de remarquable entre ce tableau et le parcours en largeur ?
4) Appliquez à nouveau cet algorithme au graphe ci-dessous en prenant A comme nœud initial.

Parcours en profondeur
Voici maintenant un algorithme qui propose un parcours en profondeur :
VARIABLES
nœud : nœud de départ (origine)
DEBUT
profondeur(nœud):
nœud.visite = True
afficher nœud
pour chaque y adjacent à nœud:
si y.visite est Faux:
profondeur(y)
FIN
5) Quelle est la particularité de ce programme par rapport au parcours en largeur ?
6) Appliquez cet algorithme au graphe ci-dessous en partant de A.

7) Appliquez à nouveau cet algorithme au graphe ci-dessous en prenant A comme nœud initial.

Chemin
Il est souvent nécessaire de trouver un chemin entre deux nœuds d’un graphe. Voici un algorithme qui permet de faire cette recherche :
VARIABLES
graphe : le graphe
start : nœud de départ (origine)
end : nœud d'arrivée
chaine : chemin initialement vide
DEBUT
trouve-chaine(graphe, start, end, chaine)
ajouter start à chaine
si start = end:
retourner chaine
pour chaque y adjacent à start:
si y n'appartient pas à chaine:
chemin = trouve-chaine(graphe, y, end, chaine)
si chemin est non-vide
retourner chemin
retourner None
FIN
8) Appliquez rigoureusement cet algorithme au graphe ci-dessous entre A et C.

9) Appliquez à nouveau cet algorithme au graphe ci-dessous entre A et C.

Cycle
Un cycle est une suite d’arrêtes (donc une chaine) dont les deux extrémités sont identiques.
Il est parfois intéressant de savoir si un graphe contient un cycle. Par exemple un graphe qui contient un cycle ne peut pas être un arbre.
Voici donc un algorithme qui permet de détecter s’il y a au moins un cycle dans un graphe :
VARIABLES
graphe : le graphe
d : le nœud de départ
p : pile
DEBUT
trouve-cycle(graphe, d)
p.empile(d)
tant que p n'est pas vide:
x = p.depile()
pour chaque y adjacent à x:
si y.visite est Faux:
p.empile(y)
si x.visite est Vrai:
retourner Vrai
sinon:
x.visite = Vrai
retourner Faux
FIN
10) Appliquez cet algorithme au graphe en haut de page en prenant A comme nœud initial.
11) Appliquez à nouveau cet algorithme au graphe ci-dessous en prenant A comme nœud initial.

implémentations : programmes de référence
Programme 1 —Parcours en profondeur
def parcours(g, vus, s):
"""parcours en profondeur depuis le sommet s"""
if s not in vus:
vus.add(s)
for v in g.voisins(s):
parcours(g, vus, v)
def existe_chemin(g, u, v):
"""existe-t-il un chemin de u à v ?"""
vus = set()
parcours(g, vus, u)
return v in vus
Programme 2 — Parcours en profondeur avec une pile
def parcours(g, vus, s):
"""parcours en profondeur depuis le sommet s"""
pile = Pile()
pile.empiler(s)
while not pile.est_vide():
s = pile.depiler()
if s in vus:
continue
vus.add(s)
for v in g.voisins(s):
pile.empiler(v)
Programme 3 — Détecter la présence d’un cycle dans un graphe
BLANC, GRIS, NOIR = 1, 2, 3
def parcours_cy(g, couleur, s):
"""parcours en profondeur depuis le sommet s"""
if couleur[s] == GRIS:
return True
if couleur[s] == NOIR:
return False
couleur[s] = GRIS
for v in g.voisins(s):
if parcours_cy(g, couleur, v):
return True
couleur[s] = NOIR
return False
def cycle(g):
couleur = {}
for s in g.sommets():
couleur[s] = BLANC
for s in g.sommets():
if parcours_cy(g, couleur, s):
return True
return False
Programme 4 — Parcours en largeur
def parcours_largeur(g, source):
"""parcours en largeur depuis le sommet source"""
dist = {source: 0}
courant = {source}
suivant = set()
while len(courant) > 0:
s = courant.pop()
for v in g.voisins(s):
if v not in dist:
suivant.add(v)
dist[v] = dist[s] + 1
if len(courant) == 0:
courant, suivant = suivant, set()
return dist
def distance(g, u, v):
"""distance de u à v (et None si pas de chemin)"""
dist = parcours_largeur(g, u)
return dist[v] if v in dist else None
Exercices
Exercice 1
Dérouler à la main le parcours en profondeur sur le graphe suivant
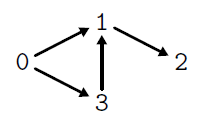
pour différentes valeurs du sommet de départ. Donner à chaque fois la valeur finale de l’ensemble vus, c’est-à-dire l’ensemble des sommets atteints par le
parcours.
Exercice 2
Dérouler à la main le parcours en largeur sur le graphe suivant
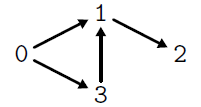
pour différentes valeurs du sommet de départ. Donner à chaque fois la valeur finale du dictionnaire dist, c’est-à-dire la distance à la source de chaque
sommet atteint par le parcours.
Exercice 3
On peut se servir d’un parcours en profondeur pour déterminer si un graphe non orienté est connexe, c’est-à-dire si tous ses sommets
sont reliés entre eux par des chemins. Pour cela, il suffit de faire un parcours en profondeur à partir d’un sommet quelconque, puis de vérifier
que tous les sommets ont été atteints par ce parcours. Écrire une fonction est_connexe() qui réalise cet algorithme. On pourra se servir de la méthode
sommets() de la classe Graphe et de la fonction parcours du programme de référence 1 voir plus haut .
Exercice 4
Dans cet exercice, on se propose d’utiliser le parcours en profondeur pour construire un chemin entre deux sommets, lorsque c’est possible.
On le fait avec deux fonctions, comme dans le programme de référence 1 voir plus haut.
def parcours_ch(g, vus, org, s):
"""parcours depuis le sommet s, en venant de org"""
…
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
…
L’idée est que l’attribut vus n’est plus un ensemble mais un dictionnaire, qui associe à chaque sommet visité le sommet qui a permis de l’atteindre
pendant le parcours en profondeur. La fonction parcours_ch prend un argument supplémentaire, org (pour origine), qui est justement le sommet qui
a permis d’atteindre s, en empruntant l’arc org → s. Écrire le code de la fonction parcours_ch ; il est très semblable à celui de la fonction parcours
du programme de référence n°1 . Écrire ensuite le code de la fonction chemin qui renvoie un chemin entre les sommets u et v, le cas échéant, et None s’il n’existe pas de chemin entre ces deux sommets. Pour cela, lancer un parcours en profondeur à partir du sommet u, en donnant à org la valeur None, puis, si le sommet v a été atteint, construire le chemin dans un tableau en« remontant » le dictionnaire vus de v jusqu’à u.
Exercice 5
Dans cet exercice, on se propose d’utiliser le parcours en largeur pour construire un chemin de longueur minimale entre deux sommets.
On le fait avec deux fonctions, comme dans le programme de référence n°4.
def parcours_largeur_ch(g, source):
"""parcours depuis le sommet source"""
…
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
…
L’idée est qu’un dictionnaire vus remplace le dictionnaire dist. Ce dictionnaire vus associe à chaque sommet visité le sommet qui a permis
de l’atteindre pendant le parcours en largeur. Écrire le code de la fonction parcours_largeur_ch ; il est très semblable à celui de la fonction
parcours_largeur du programme de référence 4. Pour le sommet source, on lui associe la valeur None dans le dictionnaire vus. Écrire ensuite le code de la fonction chemin qui renvoie un chemin réalisant la distance entre les sommets u et v, le cas échéant, et None s’il n’existe pas de chemin entre ces deux
sommets. Pour cela, lancer un parcours en largeur à partir du sommet u puis, si le sommet v a été atteint, construire le chemin dans un tableau
en« remontant » le dictionnaire vus de v jusqu’à u.
Exercice 6
Les nœuds d’un arbre binaire peuvent être vus comme les sommets d’un graphe non orienté. En particulier, on peut donc parcourir les nœuds d’un arbre avec un parcours en profondeur ou en largeur. Pour le parcours en profondeur, il s’agit d’un parcours que nous avons déjà présenté, à savoir le parcours préfixe . Dans cet exercice, on se propose de parcourir les nœuds d’un arbre binaire avec un parcours en largeur.
Écrire une fonction largeur(a) qui reçoit un arbre binaire a en argument et imprime les valeurs de ses différents nœuds dans un ordre donné par un
parcours en largeur, c’est-à-dire la valeur contenue dans la racine, puis les valeurs contenues dans les nœuds immédiatement en-dessous (profondeur 1),
puis celles contenues dans les nœuds encore en-dessous (profondeur 2), etc.
Adapter pour cela le code du programme de référence 4.
Corrections
Exercice 1
| sommet de départ | valeur finale de vus |
| 0 | {0, 1, 3, 2} |
| 1 | {1, 2} |
| 2 | {2} |
| 3 | {3, 1, 2} |
Exercice 2
| sommet de départ | valeur finale de dist |
| 0 | {0 → 0, 1 → 1, 3 → 1, 2 → 2} |
| 1 | {1 → 0, 2 → 1} |
| 2 | {2 → 0} |
| 3 | {3 → 0, 1 → 1, 2 → 2} |
Exercice 3
On suit l’algorithme proposé, en faisant uniquement attention au cas pathologique d’un graphe qui ne contiendrait aucun
sommet.
def est_connexe(g):
"""le graphe est-il connexe ?
(uniquement pour un graphe non orienté)"""
ts = g.sommets()
if len(ts) == 0:
return True
s = ts.pop()
vus = set()
parcours(g, vus, s)
for s in ts:
if s not in vus:
return False
return True
Exercice 4
Pour parcours_ch, l’ajout dans un ensemble devient un ajout dans un dictionnaire.
def parcours_ch(g, vus, org, s):
"""parcours depuis le sommet s, en venant de org"""
if s not in vus:
vus[s] = org
for v in g.voisins(s):
parcours_ch(g, vus, s, v)
Pour chemin, on prend soin de tester si v a été atteint par le parcours. Dans le cas contraire, on renvoie None. Sinon, on construit le chemin avec une
boucle while.
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
vus = {}
parcours_ch(g, vus, None, u)
if v not in vus:
return None
ch = []
s = v
while s is not None:
ch.append(s)
s = vus[s]
ch.reverse()
return ch
De fait, le chemin est construit à l’envers. On prend soin de le renverser avec la méthode reverse avant de le renvoyer.
Exercice 5
On garde la structure du programme 4, le dictionnaire vus prenant la place du dictionnaire dist.
def parcours_largeur_ch(g, source):
"""parcours depuis le sommet source"""
vus = {source: None}
courant = {source}
suivant = set()
while len(courant) > 0:
s = courant.pop()
for v in g.voisins(s):
if v not in vus:
suivant.add(v)
vus[v] = s
if len(courant) == 0:
courant, suivant = suivant, set()
return vus
La seconde partie, à savoir la reconstruction du chemin, n’est pas différente de celle effectuée dans l’exercice précédent pour un parcours en profondeur.
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
vus = parcours_largeur_ch(g, u)
if v not in vus:
return None
ch = []
s = v
while s is not None:
ch.append(s)
s = vus[s]
ch.reverse()
return ch
Exercice 6
La subtilité consiste ici à correctement traiter les arbres vides. On a le choix de le faire avant ou après l’insertion dans les ensembles.
On choisit ici de le faire après, ce qui évite de faire un cas particulier pour un arbre qui serait intégralement vide.
def largeur(a):
courant = []
suivant = []
courant.append(a)
while len(courant) > 0:
n = courant.pop()
if n is None:
continue
print(n.valeur)
suivant.append(n.gauche)
suivant.append(n.droit)
if len(courant) == 0:
courant, suivant = suivant, []