Algorithme de parcours
Un parcours de graphe est un algorithme consistant à explorer tous les sommets d’un graphe de proche en proche à partir d’un sommet initial donné. Cela généralise les parcours des arbres binaires que vous avez déjà vus.
Ces parcours sont notamment utilisés pour rechercher un plus court chemin (routage sur Internet, applications de navigation dans un réseau de métros ou de trains) ou pour trouver la sortie d’un labyrinthe.
1. Parcours de graphes, en version intuitive⚓︎
Parcours en largeur
Dans un parcours en largeur, on progresse par « cercles concentriques » à partir du sommet de départ. On visite d’abord tous les sommets à une distance de 1 unité du point départ, puis tous les sommets à une distance de 2 unités, etc. (en considérant que la distance est le nombre d’arêtes).
Par exemple, avec le graphe suivant,
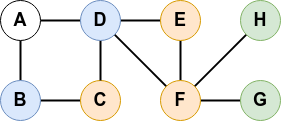
le parcours en largeur au départ de A donne la liste suivante des sommets :
A ; B ; D ; C ; E ; F ; G ; H
(avec la convention que, quand il y a plusieurs sommets à la même distance, on les écrit dans l’ordre alphabétique).
Exercice 1
Effectuer le parcours en largeur du graphe représenté ci-dessous, en partant du sommet A.
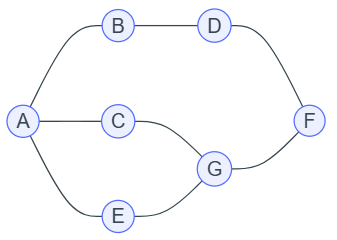
Solution
Le résultat du parcours en largeur est : A ; B ; C ; E ; D ; G ; F.
Exercice 2
Effectuer le parcours en largeur du graphe représenté ci-dessous, en partant du sommet D.
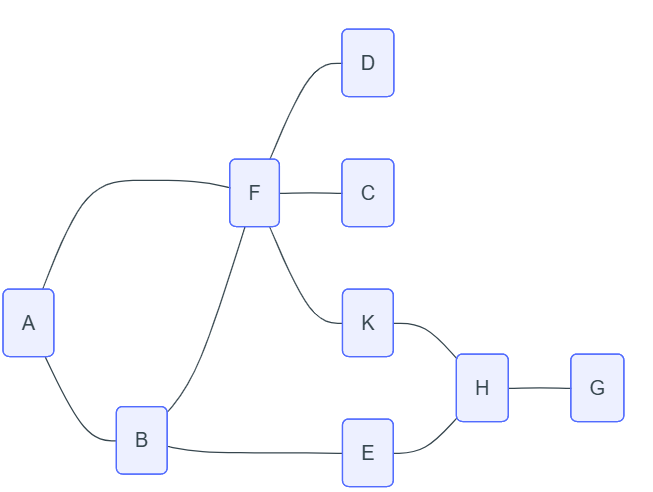
Solution
Le résultat du parcours en largeur est : D ; F ; A ; B ; C ; K ; E ; H ; G.
Parcours en profondeur
Dans un parcours en profondeur, l’idée est de suivre un chemin le plus loin possible. Si on arrive au bout d’un chemin, on revient à la bifurcation précédente pour explorer un nouveau chemin.
Par exemple, avec le graphe suivant :
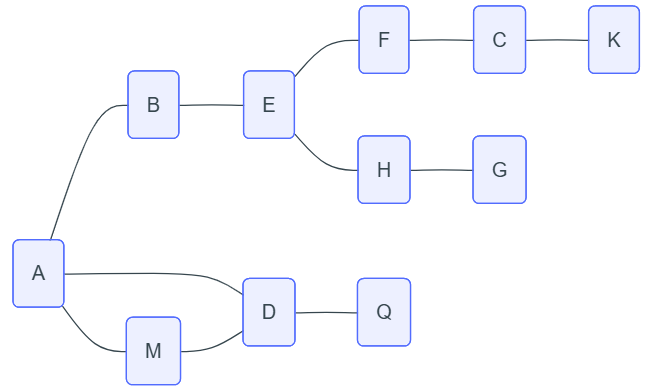
un parcours en profondeur au départ du sommet A donne :
A ; B ; E ; F ; C ; K ; H ; G ; D ; Q ; M.
Exercice
Le mécanisme d’un parcours en profondeur est encore plus explicite dans le cas des graphes orientés.
Effectuer le parcours en profondeur du graphe représenté ci-dessous, en partant du sommet A.
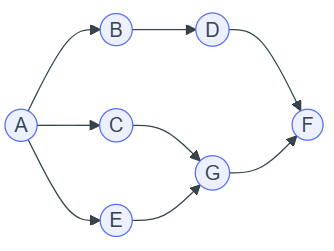
Solution
Le résultat du parcours en profondeur est : A ; E ; G ; F ; C ; B ; D.
2. Parcours de graphes, en version rigoureuse⚓︎
Algorithme de parcours
Les deux types de parcours (en largeur et en profondeur) reposent sur le même principe de base :
- Le sommet de départ
depétant donné, on crée une structureVqui contiendra au départ uniquement ce sommetdep. - Tant que
Vn’est pas vide :- on choisit un sommet
sexistant dansV; - on visite
s, c’est-à-dire qu’on l’affiche ; - on ajoute à
Vtous les voisins despas encore découverts.
- on choisit un sommet
La structure V sert donc à mémoriser les sommets qui ont été découverts mais pas encore visités.
- Si on choisit une file (FIFO), on visitera les sommets dans l’ordre d’arrivée, donc les plus proches du sommet précédent. On obtient donc un parcours en largeur ( Breadth First Search, ou BFS).
- Si on choisit une pile (LIFO), on visitera d’abord les derniers sommets arrivés, donc on parcourt le graphe en visitant à chaque étape un voisin du précédent. On obtient donc un parcours en profondeur ( Depth First Search, ou DFS).
2.1. Le parcours en largeur⚓︎
Exemple de parcours en largeur
Voici une illustration du parcours en largeur d’un graphe avec B comme sommet de départ :
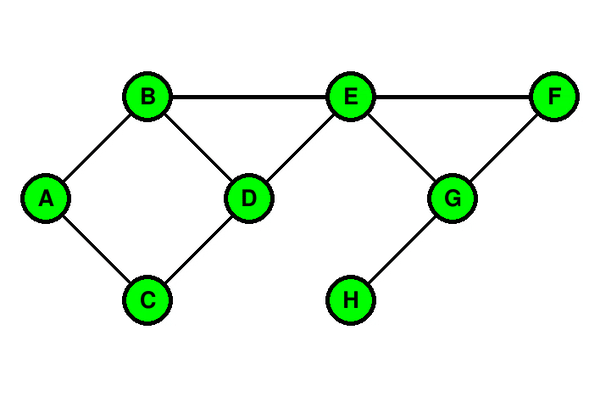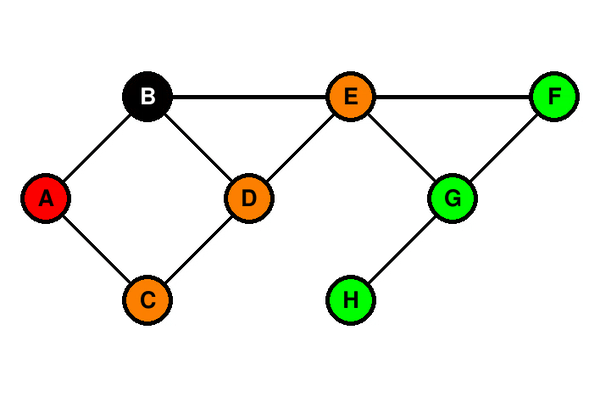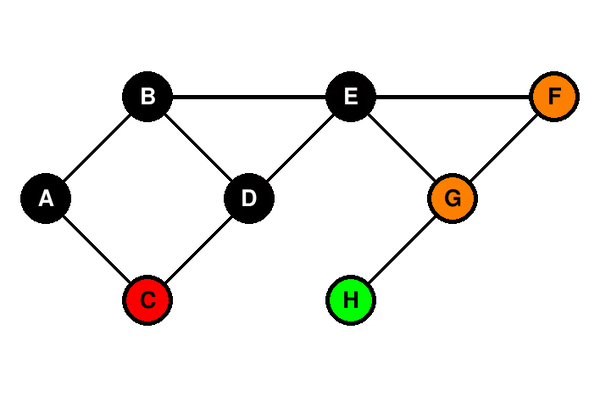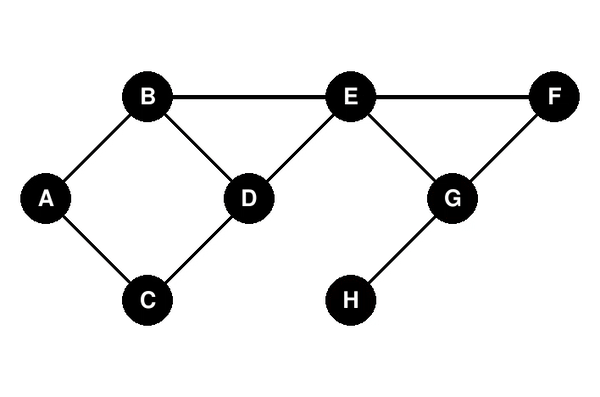
Codes couleur :
- vert : les sommets non encore traités.
- rouge : le sommet en cours de traitement.
- orange : la file d’attente des sommets qui seront bientôt traités. On y rajoute à chaque fois les voisins du sommet en cours de traitement, uniquement si ils n’ont pas encore été découverts.
- noir : les sommets traités.
Le résultat du parcours en largeur du graphe est donc : B ; A ; D ; E ; C ; F ; G ; H
Remarque : quand on ajoute plusieurs voisins d’un seul coup dans la file, on fait ici le choix de les ajouter dans l’ordre alphabétique.
Un outil en ligne
Un outil en ligne, permet de visualiser le résultat du parcours en profondeur (DFS : depth first search) d’un graphe.
Un graphe est donné en exemple, mais vous pouvez le modifier ou construire le vôtre :
Dans les menus déroulants, bien choisir Algorithm : BFS et Example graph : directedGraph
2.2. Codage d’un parcours en largeur en Python⚓︎
Remarque : ce code est donné uniquement à titre illustratif : il n’est pas nécessaire de l’apprendre par cœur. Par ailleurs, dans une partie cachée, il y a le codage des primitives des files et des graphes.
def parcours_largeur(G,s):
f = creer_file_vide()
enfiler(f,s)
tab_decouverts = [s]
while not est_vide(f):
s = defiler(f)
print(s, end=" - ")
for v in liste_voisins(G,s) :
if v not in tab_decouverts :
enfiler(f,v)
tab_decouverts.append(v)
return None
# modélisation du graphe par un dictionnaire
graphe = {"B" : ["A", "D", "E"], "A" : ["B", "C"], "C" : ["A", "D"], "D":["B", "C", "E"],
"E" : ["B", "F", "G"], "F" : ["E", "G"], "G" : ["E", "F", "H"], "H":["G"]}
# parcours du graphe
parcours_largeur(graphe, "B")
2.3. Le parcours en profondeur⚓︎
Exemple de parcours en profondeur
Rappel : dans un parcours en profondeur, chaque nouveau voisin découvert est ajouté au sommet d’une pile.
On prend comme exemple le même graphe que dans l’exemple précédent, avec un départ du sommet B. On convient que, quand il y a plusieurs sommets à empiler en même temps, on les empile dans l’ordre alphabétique.
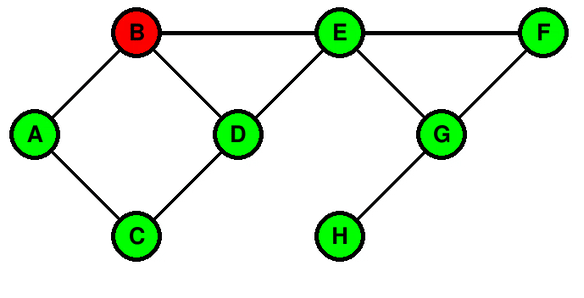
- B est visité et on empile les voisins de B : la pile contient alors A (bas de la pile), D, E (sommet de la pile).
- E est dépilé (il est visité) et on empile ses voisins qui ne sont pas déjà dans la pile : la pile contient alors A (bas de la pile), D, F, G (sommet de la pile).
- G est dépilé (il est visité) et on empile H, son seul voisin pas encore découvert : la pile contient alors A (bas de la pile), D, F, H (sommet de la pile).
- H est dépilé et il n’y a pas de nouveau voisins à empiler : la pile contient alors A (bas de la pile), D, F (sommet de la pile).
- et ainsi de suite
Au final, on obtient l’ordre de visite suivant : B ; E ; G ; H ; F ; D ; C ; A.
2.4. Codage d’un parcours en profondeur en Python⚓︎
Remarque : ce code est donné uniquement à titre illustratif : il n’est pas nécessaire de l’apprendre par cœur.
def parcours_profondeur(G,s):
p = creer_pile_vide()
empiler(p,s)
tab_decouverts = [s]
while not est_vide(p):
s = depiler(p)
print(s, end=" - ")
for v in liste_voisins(G,s) :
if v not in tab_decouverts :
empiler(p,v)
tab_decouverts.append(v)
return None
# modélisation du graphe par un dictionnaire
graphe = {"B" : ["A", "D", "E"], "A" : ["B", "C"], "C" : ["A", "D"], "D":["B", "C", "E"],
"E" : ["B", "F", "G"], "F" : ["E", "G"], "G" : ["E", "F", "H"], "H":["G"]}
# parcours du graphe
parcours_profondeur(graphe, "B")
2.5. Applications⚓︎
Graphe connexe ou pas ?
On donne ci-dessous le code d’un graphe non orienté graphe1.
En comparant les résultats des appels des fonctions liste_sommets et parcours depuis le sommet A (soit en largeur, soit en profondeur), déterminer si ce graphe est connexe ou pas.
# modélisation d'un graphe par un dictionnaire
graphe1 = {"A": ["C", "H", "I"],"B": ["J", "L"],"C": ["A", "D", "G", "I"],"D": ["C", "E"],
"E": ["D", "H"], "F": ["G", "H"], "G": ["C", "F"], "H": ["A", "E", "F"], "I": ["A", "C"],
"J": ["B", "K", "L"], "K": ["J"], "L": ["B", "J"]}
# ce graphe non orienté est-il connexe ?
Solution : On observe que le parcours du graphe depuis le sommet A fournit moins de sommets que la liste des sommets. Ce graphe n’est donc pas connexe.
Sommet atteignable ou pas ?
On donne ci-dessous le code d’un graphe connexe orienté graphe2.
En effectuant un parcours depuis le sommet A (soit en largeur, soit en profondeur), déterminer s’il est possible d’atteindre le sommet B depuis ce sommet A.
Ce même sommet B est-il atteignable depuis le sommet N ?
# modélisation d'un graphe par un dictionnaire
graphe2 = {
"A": ["G", "K", "L"], "B": ["L", "N"], "C": ["A", "D", "I"], "D": ["C"], "E": ["D", "F", "G"],
"F": ["H"], "G": ["D"], "H": ["E", "G"], "I": ["A", "G", "H"], "J": ["B", "M", "N"],
"K": ["I"], "L": [], "M": ["B"], "N": ["M"]
}
# dans ce graphe orienté, est-il possible d'aller de A vers B ? et de N vers B ?
Solution
On observe que le sommet B n’apparait pas dans le parcours du graphe depuis le sommet A : B n’est donc pas atteignable depuis A.
Mais B est atteignable depuis le sommet N, comme le montre un parcours depuis N.
3. TP: graphe et labyrinthe⚓︎
Télécharger le carnet Jupyter, à ouvrir sur Basthon.
Il faudra aussi charger dans Basthon les trois modules Python suivants (Ouvrir… puis Installer le module) : laby2d.py, laby3d.py et solution.py.
4. Algorithme de recherche d’un plus court chemin : algorithme de Dijkstra⚓︎
Vous avez déjà effectué la recherche d’un plus court chemin dans un graphe pondéré, quand il s’agissait de trouver le chemin emprunté pour aller d’un routeur A à un routeur B selon le protocole OSPF.
On peut systématiser la détermination du plus court chemin d’un point à un autre en appliquant l’algorithme de Dijkstra (mis au point par Edsger Dijkstra en 1959), comme expliqué dans la vidéo suivante :
Application de l’algorithme de Dijkstra
Donner le plus court chemin pour aller de E à F dans le graphe ci-dessous :
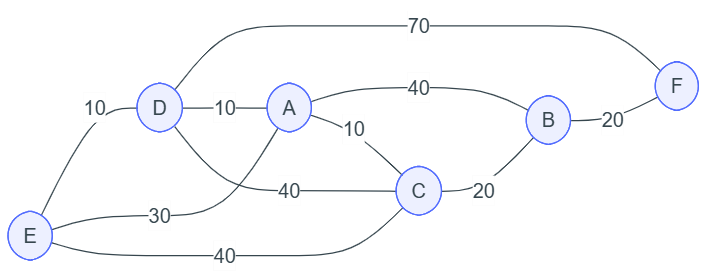
Solution
| E | A | B | C | D | F | Choix |
|---|---|---|---|---|---|---|
| 0 | — | — | — | — | — | E(0) |
| . | 30 vE | — | 40 vE | 10 vE | — | D(10) |
| . | 20 vD | — | 40 vE | . | 80 vD | A(20) |
| . | . | 60 vA | 30 vA | . | 80 vD | C(30) |
| . | . | 50 vC | . | . | 80 vD | B(50) |
| . | . | . | . | . | 70 vB | F(70) |
Le meilleur trajet est donc E-D-A-C-B-F, pour une distance totale de 70.
Attention ce trajet correspond à la colonne choix (dans l’ordre) mais ce n’est pas toujours le cas.
Deuxième application de l’algorithme de Dijkstra
Déterminer le plus court chemin entre A et G dans le graphe pondéré ci-dessous (en version papier).
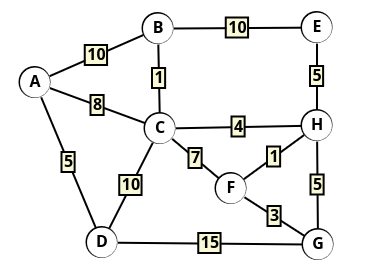
Solution
| A | B | C | D | E | F | G | H | Choix |
|---|---|---|---|---|---|---|---|---|
| 0 | — | — | — | — | — | — | — | A(0) |
| . | 10 vA | 8 vA | 5 vA | — | — | — | — | D(5) |
| . | 10 vA | 8 vA | . | — | — | 20 vD | — | C(8) |
| . | 9 vC | . | . | — | 15 vC | 20 vD | 12 vC | B(9) |
| . | . | . | . | 19 vB | 15 vD | 20 vD | 12 vC | H(12) |
| . | . | . | . | 17 vH | 13 vH | 17 vH | . | F(13) |
| . | . | . | . | 17 vH | . | 16 vF | . | G(16) |
Le meilleur trajet est donc A – C – H – F – G, pour une distance totale de 16.
L’algorithme de Dijkstra, ici exécuté de manière manuelle, est bien sûr programmable. Mais cela dépasse le niveau attendu en fin de Terminale.
5. Exercices⚓︎
programmes ressources
Graphe représenté par une matrice d’adjacence
class Graphe:
"""un graphe représenté par une matrice d’adjacence,
où les sommets sont les entiers 0,1,...,n-1"""
def __init__(self, n):
self.n = n
self.adj = [[False] * n for _ in range(n)]
def ajouter_arc(self, s1, s2):
self.adj[s1][s2] = True
def arc(self, s1, s2):
return self.adj[s1][s2]
def voisins(self, s):
v = []
for i in range(self.n):
if self.adj[s][i]:
v.append(i)
return v
Graphe représenté par un dictionnaire d’adjacence
class Graphe:
"""un graphe comme un dictionnaire d’adjacence"""
def __init__(self):
self.adj = {}
def ajouter_sommet(self, s):
if s not in self.adj:
self.adj[s] = set()
def ajouter_arc(self, s1, s2):
self.ajouter_sommet(s1)
self.ajouter_sommet(s2)
self.adj[s1].add(s2)
def arc(self, s1, s2):
return s2 in self.adj[s1]
def sommets(self):
return list (self.adj)
def voisins(self, s):
return self.adj[s]
Exercice 1 Dessiner tous les graphes non orientés ayant exactement trois sommets.
Solution : 8 au total :
Exercice 2 Combien y a-t-il de graphes orientés ayant exactement trois sommets ? On ne demande pas de les dessiner tous, mais seulement de les dénombrer.
Solution : Il y a six arcs possibles (0 → 1, 1 → 0, 1 → 2, 2 → 1, 2 → 0, 0 → 2), chacun pouvant être présent ou absent, soit possibilités au total.
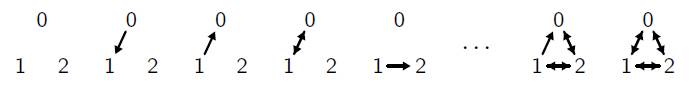
Exercice 3 Ajouter à la classe Graphe du programme matrice d’adjacence donné avant les consignes des exercices, une méthode afficher pour afficher le graphe sous la forme suivante
0 -> 1 3
1 -> 2 3
2 -> 3
3 -> 1
c’est-à-dire une ligne par sommet, avec pour chacun la liste de ses voisins.
def afficher(self):
for s in range(self.n):
print(s, "->", end="")
for v in range(self.n):
if self.adj[s][v]:
print("", v, end="")
print()
Exercice 04 Ajouter à la classe Graphe du programme dictionnaire d’adjacence donné avant les consignes des exercices une méthode afficher pour afficher le graphe sous la forme suivante
0 {1, 3}
1 {2, 3}
3 {1}
2 {3}
c’est-à-dire une ligne par sommet, avec pour chacun l’ensemble de ses voisins.
L’ordre des sommets n’est pas important. L’ensemble des voisins peut être affiché directement avec print.
Correction : On fait un cas particulier pour l’ensemble vide, histoire qu’il ne soit pas affiché comme set() mais comme {}.
def afficher(self):
for s in self.adj:
if len(self.adj[s]) == 0:
print(s, "{}")
else:
print(s, self.adj[s])
Exercice 05 Ajouter à la classe Graphe du programme dictionnaire d’adjacence donné avant les consignes des exercices une méthode nb_sommets() qui donne le nombre de sommets du graphe.
Correction : Le nombre de sommets est égal au nombre d’entrées dans le dictionnaire :
def nb_sommets(self):
return len(self.adj)
Exercice 06 Ajouter à la classe Graphe du programme matrice d’adjacence donné avant les consignes des exercices une méthode degre(s) qui donne le nombre d’arcs issus du sommet s. On appelle cela le degré du sommet s.
Correction : Le code est très semblable à celui de la méthode voisins :
def degre(self, s):
d = 0
for i in range(self.n):
if self.adj[s][i]:
d += 1
return d
Exercice 07 En utilisant l’exercice précédent, ajouter à la classe Graphe du programme matrice d’adjacence donné avant les consignes des exercices une méthode nb_arcs() qui donne le nombre total d’arcs du graphe.
Correction : Il suffit de faire la somme de tous les degrés.
def nb_arcs(self):
n = 0
for s in range(self.n):
n += self.degre(s)
return n
Exercice 08 Ajouter à la classe Graphe du programme dictionnaire d’adjacence donné avant les consignes des exercices une méthode degre(s) qui donne le nombre d’arcs issus du sommet s. On appelle cela le degré du sommet s.
Correction : C’est exactement le cardinal de l’ensemble adj[s] :
def degre(self, s):
return len(self.adj[s])
Exercice 09 En utilisant l’exercice précédent, ajouter à la classe Graphe du programme dictionnaire d’adjacence donné avant les consignes des exercices une méthode nb_arcs() qui donne le nombre total d’arcs du graphe.
Correction : comme il y a deux exercice, on fait la somme de tous les degrés.
def nb_arcs(self):
n = 0
for s in self.adj:
n += self.degre(s)
return n
Exercice 10 Ajouter aux classes Graphe des programmes dictionnaire et matrice d’adjacence une méthode supprimer_arc(s1, s2) pour supprimer l’arc entre les sommets s1 et s2. S’il n’y a pas d’arc entre ces sommets, la méthode n’a aucun effet. On supprime un élément d’un ensemble avec sa méthode remove.
Correction : Pour la matrice d’adjacence, on affecte le booléen False dans la matrice :
def supprimer_arc(self, s1, s2):
self.adj[s1][s2] = False
def supprimer_arc(self, s1, s2):
if self.arc(s1, s2):
self.adj[s1].remove(s2)
Pour le dictionnaire d’adjacence, on supprime s2 de l’ensemble des voisins de s1, si l’arc existe :
def supprimer_arc(self, s1, s2):
if self.arc(s1, s2):
self.adj[s1].remove(s2)
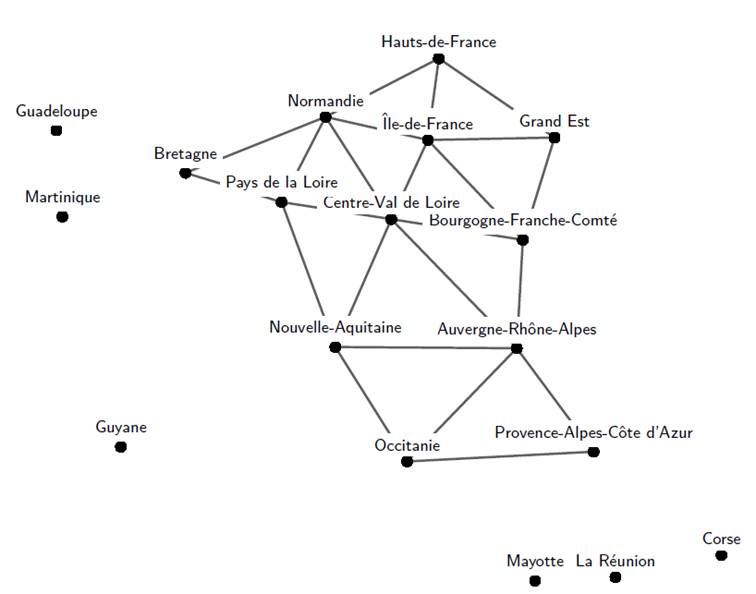
Exercice 11 Donner une coloration du graphe des régions ci-dessus qui n’utilise que quatre couleurs.
Correction : Il suffit de reprendre les couleurs obtenues avec l’algorithme glouton (figure 11.2 page 204) et de faire seulement deux changements :
Bretagne 1 (au lieu de 0)
Normandie 0 (au lieu de 4)
Exercice 12 : coloriage de graphes
écrivons un programme qui colorie un graphe avec un algorithme glouton. Colorier un graphe veut dire associer une couleur à chacun de ses sommets, de façon à ce que deux sommets reliés par un arc n’aient pas la même couleur. Colorier un graphe avec un minimum de couleurs est un problème difficile, mais si on accepte l’idée d’utiliser éventuellement plus de couleurs que nécessaire, alors on peut colorier un graphe efficacement. Le principe d’un coloriage glouton est simple. On parcourt les sommets dans un ordre arbitraire et, pour chaque sommet, on lui attribue la première couleur qui n’est pas utilisée par ses voisins.
def mex(voisins, couleur):
"""la plus petite couleur non utilisée par les voisins"""
n = len(voisins)
dispo = [True] * (n + 1)
for v in voisins:
if v in couleur and couleur[v] <= n:
dispo[couleur[v]] = False
for c in range(n + 1):
if dispo[c]:
return c
assert False # on n’arrivera jamais ici
def coloriage(g):
"""colorie graphe g avec un algorithme glouton"""
couleur = {}
n = 0
for s in g.sommets():
c = mex(g.voisins(s), couleur)
couleur[s] = c
n = max(n, c + 1)
return couleur, n
programmes de référence :
Programme 39 — Parcours en profondeur
def parcours(g, vus, s):
"""parcours en profondeur depuis le sommet s"""
if s not in vus:
vus.add(s)
for v in g.voisins(s):
parcours(g, vus, v)
def existe_chemin(g, u, v):
"""existe-t-il un chemin de u à v ?"""
vus = set()
parcours(g, vus, u)
def parcours(g, vus, s):
"""parcours en profondeur depuis le sommet s"""
if s not in vus:
vus.add(s)
for v in g.voisins(s):
parcours(g, vus, v)
def existe_chemin(g, u, v):
"""existe-t-il un chemin de u à v ?"""
vus = set()
parcours(g, vus, u)
return v in vus
Programme 40 — Parcours en profondeur avec une pile
def parcours(g, vus, s):
"""parcours en profondeur depuis le sommet s"""
pile = Pile()
pile.empiler(s)
while not pile.est_vide():
s = pile.depiler()
if s in vus:
continue
vus.add(s)
for v in g.voisins(s):
pile.empiler(v)
Programme 41 — Détecter la présence d’un cycle dans un graphe
BLANC, GRIS, NOIR = 1, 2, 3
def parcours_cy(g, couleur, s):
"""parcours en profondeur depuis le sommet s"""
if couleur[s] == GRIS:
return True
if couleur[s] == NOIR:
return False
couleur[s] = GRIS
for v in g.voisins(s):
if parcours_cy(g, couleur, v):
return True
couleur[s] = NOIR
return False
def cycle(g):
couleur = {}
for s in g.sommets():
couleur[s] = BLANC
for s in g.sommets():
if parcours_cy(g, couleur, s):
return True
return False
Programme 42 — Parcours en largeur
def parcours_largeur(g, source):
"""parcours en largeur depuis le sommet source"""
dist = {source: 0}
courant = {source}
suivant = set()
while len(courant) > 0:
s = courant.pop()
for v in g.voisins(s):
if v not in dist:
suivant.add(v)
dist[v] = dist[s] + 1
if len(courant) == 0:
courant, suivant = suivant, set()
return dist
def distance(g, u, v):
"""distance de u à v (et None si pas de chemin)"""
dist = parcours_largeur(g, u)
return dist[v] if v in dist else None
Exercice 104 Dérouler à la main le parcours en profondeur sur le graphe suivant
pour différentes valeurs du sommet de départ. Donner à chaque fois la valeur finale de l’ensemble vus, c’est-à-dire l’ensemble des sommets atteints par le parcours.
Correction :
Exercice 105 Dérouler à la main le parcours en largeur sur le graphe suivant
pour différentes valeurs du sommet de départ. Donner à chaque fois la valeur finale du dictionnaire dist, c’est-à-dire la distance à la source de chaque sommet atteint par le parcours.
Correction :
Exercice 106 On peut se servir d’un parcours en profondeur pour déterminer si un graphe non orienté est connexe, c’est-à-dire si tous ses sommets sont reliés entre eux par des chemins. Pour cela, il suffit de faire un parcours en profondeur à partir d’un sommet quelconque, puis de vérifier que tous les sommets ont été atteints par ce parcours. Écrire une fonction est_connexe() qui réalise cet algorithme. On pourra se servir de la méthode sommets() de la classe Graphe et de la fonction parcours du programme Parcours en profondeur.
Correction : On suit l’algorithme proposé, en faisant uniquement attention au cas pathologique d’un graphe qui ne contiendrait aucun sommet.
def est_connexe(g):
"""le graphe est-il connexe ?
(uniquement pour un graphe non orienté)"""
ts = g.sommets()
if len(ts) == 0:
return True
s = ts.pop()
vus = set()
parcours(g, vus, s)
for s in ts:
if s not in vus:
return False
return True
Exercice 107 Dans cet exercice, on se propose d’utiliser le parcours en profondeur pour construire un chemin entre deux sommets, lorsque c’est possible. On le fait avec deux fonctions, comme dans le programme Parcours en profondeur.
def parcours_ch(g, vus, org, s):
« » »parcours depuis le sommet s, en venant de org » » »
…
def chemin(g, u, v):
« » »un chemin de u à v, le cas échéant, None sinon » » »
…
L’idée est que l’attribut vus n’est plus un ensemble mais un dictionnaire, qui associe à chaque sommet visité le sommet qui a permis de l’atteindre pendant le parcours en profondeur. La fonction parcours_ch prend un argument supplémentaire, org (pour origine), qui est justement le sommet qui a permis d’atteindre s, en empruntant l’arc org → s. Écrire le code de la fonction parcours_ch ; il est très semblable à celui de la fonction parcours du programme 39. Écrire ensuite le code de la fonction chemin qui renvoie un chemin entre les sommets u et v, le cas échéant, et None s’il n’existe pas de chemin entre ces deux sommets. Pour cela, lancer un parcours en profondeur à partir du sommet u, en donnant à org la valeur None, puis, si le sommet v a été atteint, construire le chemin dans un tableau en« remontant » le dictionnaire vus de v jusqu’à u.
Correction : Pour parcours_ch, l’ajout dans un ensemble devient
un ajout dans un dictionnaire.
def parcours_ch(g, vus, org, s):
"""parcours depuis le sommet s, en venant de org"""
if s not in vus:
vus[s] = org
for v in g.voisins(s):
parcours_ch(g, vus, s, v)
Pour chemin, on prend soin de tester si v a été atteint par le parcours. Dans le cas contraire, on renvoie None. Sinon, on construit le chemin avec une boucle while.
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
vus = {}
parcours_ch(g, vus, None, u)
if v not in vus:
return None
ch = []
s = v
while s is not None:
ch.append(s)
s = vus[s]
ch.reverse()
return ch
De fait, le chemin est construit à l’envers. On prend soin de le renverser avec la méthode reverse avant de le renvoyer.
Exercice 108 Dans cet exercice, on se propose d’utiliser le parcours en largeur pour construire un chemin de longueur minimale entre deux sommets. On le fait avec deux fonctions, comme dans le programme Parcours en largeur.
def parcours_largeur_ch(g, source):
« » »parcours depuis le sommet source » » »
…
def chemin(g, u, v):
« » »un chemin de u à v, le cas échéant, None sinon » » »
…
L’idée est qu’un dictionnaire vus remplace le dictionnaire dist. Ce dictionnaire vus associe à chaque sommet visité le sommet qui a permis de l’atteindre pendant le parcours en largeur. Écrire le code de la fonction parcours_largeur_ch ; il est très semblable à celui de la fonction parcours_largeur du programme 42. Pour le sommet source, on lui associe la valeur None dans le dictionnaire vus. Écrire ensuite le code de la fonction chemin qui renvoie un chemin réalisant la distance entre les sommets u et v, le cas échéant, et None s’il n’existe pas de chemin entre ces deux sommets. Pour cela, lancer un parcours en largeur à partir du sommet u puis, si le sommet v a été atteint, construire le chemin dans un tableau en« remontant » le dictionnaire vus de v jusqu’à u.
Correction : On garde la structure du programme 42, le dictionnaire vus prenant la place du dictionnaire dist.
def parcours_largeur_ch(g, source):
"""parcours depuis le sommet source"""
vus = {source: None}
courant = {source}
suivant = set()
while len(courant) > 0:
s = courant.pop()
for v in g.voisins(s):
if v not in vus:
suivant.add(v)
vus[v] = s
if len(courant) == 0:
courant, suivant = suivant, set()
return vus
La seconde partie, à savoir la reconstruction du chemin, n’est pas différente de celle effectuée dans l’exercice précédent pour un parcours en profondeur.
def chemin(g, u, v):
"""un chemin de u à v, le cas échéant, None sinon"""
vus = parcours_largeur_ch(g, u)
if v not in vus:
return None
ch = []
s = v
while s is not None:
ch.append(s)
s = vus[s]
ch.reverse()
return ch
Exercice 109 Les nœuds d’un arbre binaire peuvent être vus comme les sommets d’un graphe non orienté. En particulier, on peut donc parcourir largeur les nœuds d’un arbre avec un parcours en profondeur ou en largeur. Pour le parcours en profondeur, il s’agit d’un parcours que nous avons déjà présenté, à savoir le parcours préfixe . Dans cet exercice, on se propose de parcourir les nœuds d’un arbre binaire avec un parcours en largeur.
Écrire une fonction largeur(a) qui reçoit un arbre binaire a en argument et imprime les valeurs de ses différents nœuds dans un ordre donné par un parcours en largeur, c’est-à-dire la valeur contenue dans la racine, puis les valeurs contenues dans les nœuds immédiatement en-dessous (profondeur 1), puis celles contenues dans les nœuds encore en-dessous (profondeur 2), etc.
Adapter pour cela le code du programme Parcours en largeur.
Correction
La subtilité consiste ici à correctement traiter les arbres vides. On a le choix de le faire avant ou après l’insertion dans les ensembles.
On choisit ici de le faire après, ce qui évite de faire un cas particulier pour un arbre qui serait intégralement vide.
def largeur(a):
courant = []
suivant = []
courant.append(a)
while len(courant) > 0:
n = courant.pop()
if n is None:
continue
print(n.valeur)
suivant.append(n.gauche)
suivant.append(n.droit)
if len(courant) == 0:
courant, suivant = suivant, []