1. Les Listes Chaînées : La Chasse au Trésor ! 🗺️
Imagine tes données non pas comme des objets sagement alignés, mais plutôt comme des indices pour une chasse au trésor ! Chaque indice (un morceau de donnée) ne te dit pas où se trouve le prochain élément juste en étant à côté de lui. Non ! Chaque indice contient une petite note secrète : l’adresse de l’indice suivant !
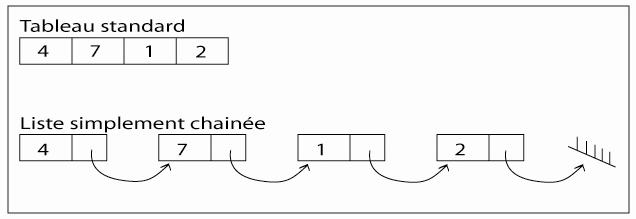
C’est ça, une liste chaînée !
- Chaque élément, qu’on appelle souvent un nœud, est comme une petite boîte à deux compartiments :
- Le premier compartiment contient la valeur de l’élément (ton trésor !).
- Le deuxième compartiment contient une flèche (un pointeur) vers la boîte suivante.

Le dernier élément ? Sa flèche pointe vers None (ou Null), pour dire « fin de la chaîne, plus d’indices ici ! ».
La Magie de la Flexibilité : Insérer et Supprimer sans Déménager ! ✨
L’énorme avantage des listes chaînées, c’est leur flexibilité. Si tu veux ajouter un nouvel indice au milieu de ta chasse au trésor, tu n’as pas besoin de tout réorganiser ! Tu changes juste quelques flèches :
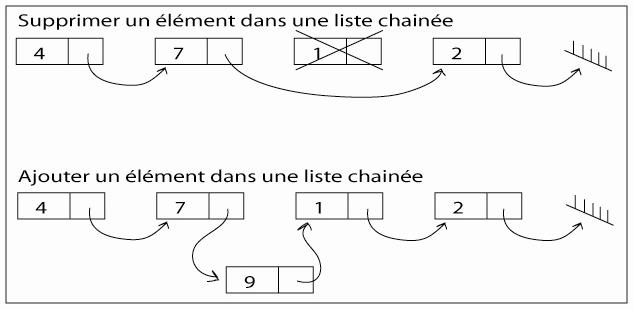
Pareil pour supprimer : tu « sautes » juste l’élément en question en refaisant pointer la flèche précédente vers l’élément suivant. Facile comme bonjour !
2. Les Listes (Abstraites) : Le Serpentin Flexible de Tes Données 🐍
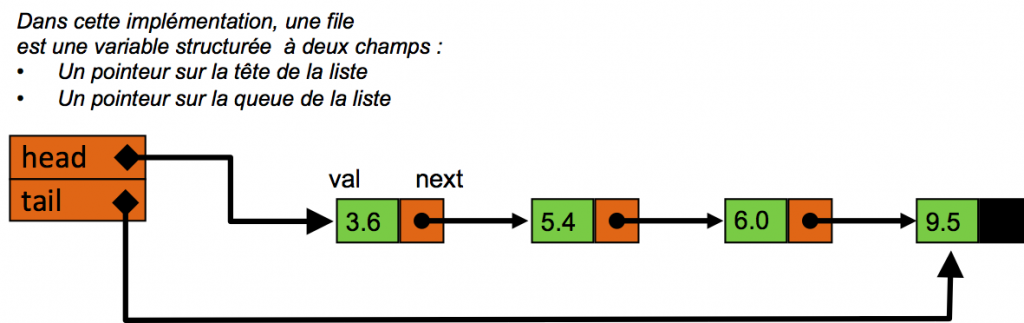
Maintenant que tu as compris la mécanique interne des listes chaînées, parlons du concept de « Liste » tel qu’il a été popularisé par des langages comme Lisp (qui veut dire « List Processing » !). Pour Lisp, et pour nous en NSI, une liste est une structure de données logique, un Type Abstrait de Données (TAD), dont la particularité est d’avoir une « tête » et une « queue », un peu comme un serpentin :
- Tête (Head ou
caren Lisp) : Le premier élément. C’est l’entrée principale du serpentin. - Queue (Tail ou
cdren Lisp) : Le reste de la liste, sans la tête. C’est le corps du serpentin.
Quand on parle de « Liste » dans ce sens abstrait, on ne se soucie pas de comment elle est vraiment construite (chaînée, tableau dynamique, etc.). On se concentre sur les opérations qu’on peut faire dessus :
creer_liste_vide(): Pour commencer avec un serpentin sans aucun wagon.est_vide(ma_liste): Pour vérifier si le serpentin a des wagons ou non.ajouter_en_tete(element, ma_liste): Tu ajoutes un nouveau wagon à la tête du serpentin. L’ancien premier wagon devient le nouveau deuxième.supprimer_en_tete(ma_liste): Tu détaches le wagon de tête et tu le récupères. Le serpentin se raccourcit.compter_elements(ma_liste): Pour connaître la longueur de ton serpentin.construire_liste(element, ancienne_liste)(le célèbreconsde Lisp) : C’est une opération fondamentale ! Elle prend unelementet uneancienne_liste, et renvoie une NOUVELLE LISTE où l’elementest en tête et l’ancienne_listeest sa queue. C’est super pour « construire » des listes petit à petit ou les transformer sans modifier l’originale :construire_liste(x, construire_liste(y, construire_liste(z, liste_vide))).
Exemples Concrets : La Vie de Nos Listes Abstraites !
Voici un scénario d’aventures pour nos listes :
L = creer_liste_vide()- Action : On initialise une liste toute seule, sans rien.
- État de L :
[](vide)
est_vide(L)- Action : On vérifie si
Lest vide. - Résultat :
True
- Action : On vérifie si
L = ajouter_en_tete(3, L)- Action : On ajoute le chiffre 3 en tête de
L. C’est le premier (et seul) élément. - État de L :
[3](tête: 3, queue: vide)
- Action : On ajoute le chiffre 3 en tête de
est_vide(L)- Action : On revérifie.
- Résultat :
False
L = ajouter_en_tete(5, L)- Action : Le 5 arrive en tête ! Le 3 passe en queue.
- État de L :
[5, 3](tête: 5, queue: [3])
L = ajouter_en_tete(8, L)- Action : Le 8 prend la place du 5.
- État de L :
[8, 5, 3](tête: 8, queue: [5, 3])
t = supprimer_en_tete(L)- Action : On retire le 8 de la tête. Il nous est retourné.
- Valeur de t :
8 - État de L :
[5, 3](tête: 5, queue: [3])
L1 = creer_liste_vide()- Action : Une nouvelle liste, L1, est créée, vide.
- État de L1 :
[]
L2 = construire_liste(8, construire_liste(5, construire_liste(3, L1)))- Action : On utilise notre sort
construire_listepour créer L2. construire_liste(3, L1)donne[3]construire_liste(5, [3])donne[5, 3]construire_liste(8, [5, 3])donne[8, 5, 3]- État de L2 :
[8, 5, 3](tête: 8, queue: [5, 3])
- Action : On utilise notre sort
En programmation Objet
# Cellule d’une liste chaînée
class Cellule:
"""une cellule d’une liste chaînée"""
def __init__(self, v, s):
self.valeur = v
self.suivante = s
# longueur d'une liste chainée avec une fonction récursive
def longueur(lst):
"""renvoie la longueur de la liste lst"""
if lst is None:
return 0
else:
return 1 + longueur(lst.suivante)
# longueur d'une liste chainée avec une boucle
def longueur(lst):
"""renvoie la longueur de la liste lst"""
n = 0
c = lst
while c is not None:
n += 1
c = c.suivante
return n
# N-ième élément d’une liste
def nieme_element(n, lst):
"""renvoie le n-ième élément de la liste lst
les éléments sont numérotés à partir de 0"""
if lst is None:
raise IndexError("indice invalide")
if n == 0:
return lst.valeur
else:
return nieme_element(n - 1, lst.suivante)
# Concaténation de deux listes
def concatener(l1, l2):
"""concatène les listes l1 et l2,
sous la forme d’une nouvelle liste"""
if l1 is None:
return l2
else:
return Cellule(l1.valeur, concatener(l1.suivante,l2))
# Renverser une liste
def renverser(lst):
"""renvoie une liste contenant les éléments
de lst dans l’ordre inverse"""
r = None
c = lst
while c is not None:
r = Cellule(c.valeur, r)
c = c.suivante
return r
#Encapsulation d’une liste dans un objet
class Liste:
"""une liste chaînée"""
def __init__(self):
self.tete = None
def est_vide(self):
return self.tete is None
def ajoute(self, x):
self.tete = Cellule(x, self.tete)
def __len__(self):
return longueur(self.tete)
def __getitem__(self, n):
return nieme_element(n, self.tete)
def reverse(self):
self.tete = renverser(self.tete)
def __add__(self, lst):
r = Liste()
r.tete = concatener(self.tete, lst.tete)
return r
À faire vous-même 1 : Le Mystère de la Chaîne de Liste 🕵️♀️
Voici une série d’instructions. À toi de jouer les détectives et d’expliquer ce qui se passe à chaque étape, et quel est l’état final de chaque liste !
L = creer_liste_vide()
L = ajouter_en_tete(10,L)
L = ajouter_en_tete(9,L)
L = ajouter_en_tete(7,L)
L1 = creer_liste_vide()
L2 = construire_liste(5, construire_liste(4, construire_liste(3, construire_liste(2, construire_liste(1, construire_liste(0,L1))))))
3. Les Piles : La Tour d’Assiettes Magique ! 🍽️ (Un cas particulier de Liste)
Tu as compris les listes chaînées, et les listes « abstraites » avec leur tête et leur queue. Eh bien, une pile est une liste super stricte ! Imagine une pile d’assiettes dans ta cuisine. Quand tu ajoutes une assiette, tu la mets au-dessus des autres. Quand tu en prends une, tu prends toujours celle qui est tout en haut. Impossible de prendre une assiette du milieu sans faire tout tomber, n’est-ce pas ?
![Dessin d’une pile d’assiettes avec une flèche « Empiler » qui pointe vers le haut de la pile et une flèche « Dépiler » qui pointe vers le bas depuis le haut de la pile, illustrant l’entrée et la sortie par le même côté.]
Les piles en informatique, c’est exactement ça ! C’est le principe LIFO qui règne en maître : Last In, First Out (le dernier élément à être entré est le premier à sortir). C’est hyper courant en info (pour gérer les appels de fonctions, l’historique « annuler » dans un logiciel, etc.) !
Voici les sorts magiques (opérations) que tu peux jeter sur une pile :
pile_est_vide?(P): Pour savoir si ta pile d’assiettes est vide.empiler(P, x)(oupush(P, x)) : Tu ajoutes un nouvel élémentxtout en haut de la pile. (C’est comme unajouter_en_tete!)depiler(P)(oupop(P)) : Tu récupères l’élément qui est au sommet de la pile et tu le retires. C’est le seul qui est accessible ! (C’est comme unsupprimer_en_tete!)sommet(P)(oupeek(P)) : Tu peux juste jeter un œil à l’élément du sommet, sans le retirer de la pile. Super pour voir sans casser la tour !taille(P): Pour savoir combien d’assiettes il y a dans ta pile.
Exemples Concrets : La Vie de Nos Piles !
Repartons d’une pile P d’éléments : [12, 14, 8, 7, 19, 22] (avec 22 au sommet).
depiler(P)- Action : On retire l’assiette du dessus.
- Résultat : Renvoie
22. - État de P :
[12, 14, 8, 7, 19](19 est maintenant au sommet)
empiler(P, 42)- Action : On ajoute le 42 par-dessus tout.
- État de P :
[12, 14, 8, 7, 19, 22, 42](42 est au sommet)
sommet(P)- Action : On regarde juste le dessus.
- Résultat : Renvoie
22. - État de P :
Pn’est PAS modifiée, elle reste[12, 14, 8, 7, 19, 22](22 est toujours au sommet)
si on applique depiler(P) 6 fois de suite, pile_est_vide?(P)- Action : On vide la pile.
- Résultat : Renvoie
True.
Après avoir appliqué depiler(P) une fois, taille(P)- Action : On retire un élément, puis on compte.
- Résultat : Renvoie
5.
À faire vous-même 2 : Le Mystère du Dépilement 🧐
Soit une pile P composée des éléments suivants : [15, 11, 32, 45, 67] (le sommet de la pile est 67).
Quel est l’effet de l’instruction depiler(P) ? (Qu’est-ce que ça renvoie et quel est le nouvel état de la pile ?)
4. Les Files : La File d’Attente du Cinéma ! 🍿
Comme les piles, les files ont des points communs avec les listes, mais avec une différence cruciale : dans une file, on ajoute des éléments à une extrémité (la « queue » de la file) et on supprime des éléments à l’autre extrémité (la « tête » de la file). On prend souvent l’analogie de la file d’attente devant un magasin ou un cinéma pour décrire une file de données.
![Dessin d’une file d’attente avec une flèche « Ajouter » qui pointe vers l’arrière de la file et une flèche « Retirer » qui pointe vers l’avant de la file, illustrant l’entrée par un côté et la sortie par l’autre.]
Les files sont basées sur le principe FIFO : First In, First Out (le premier élément à être entré est le premier à sortir). C’est le principe d’équité ! Tu le retrouves partout, de la gestion des tâches d’impression aux messages dans une application.
Voici les sorts magiques (opérations) que l’on peut réaliser sur une file :
file_est_vide?(F): Pour savoir si la file d’attente est vide.ajouter(F, x)(ouenqueue(F, x)) : Tu ajoutes un nouvel élémentxà la fin de la file.retirer(F)(oudequeue(F)) : Tu récupères l’élément qui est au début de la file et tu le retires. C’est le premier qui a attendu !premier(F)(oufront(F)) : Tu peux juste jeter un œil à l’élément qui est au début de la file, sans le supprimer.taille(F): Pour savoir combien de personnes il y a dans ta file.
Exemples Concrets : La Vie de Nos Files !
Repartons d’une file F d’éléments : [22, 19, 7, 8, 14, 12] (22 est le premier élément arrivé, 12 est le dernier).
ajouter(F, 42)- Action : Le 42 arrive à la fin de la file.
- État de F :
[22, 19, 7, 8, 14, 12, 42](22 est le premier, 42 est le dernier)
retirer(F)- Action : On retire le premier arrivé.
- Résultat : Renvoie
22. - État de F :
[19, 7, 8, 14, 12](19 est maintenant le premier, 12 le dernier)
premier(F)- Action : On regarde qui est le prochain à être servi.
- Résultat : Renvoie
22. - État de F :
Fn’est PAS modifiée, elle reste[22, 19, 7, 8, 14, 12]
si on applique retirer(F) 6 fois de suite, file_est_vide?(F)- Action : On vide la file.
- Résultat : Renvoie
True.
Après avoir appliqué retirer(F) une fois, taille(F)- Action : On retire un élément, puis on compte.
- Résultat : Renvoie
5.
À faire vous-même 3 : Le Mystère de l’Ajout à la File 🤷♀️
Soit une file F composée des éléments suivants : [72, 21, 17, 24, 12, 1] (le premier élément rentré dans la file est 72 ; le dernier élément rentré dans la file est 1).
Quel est l’effet de l’instruction ajouter(F, 25) ? (Quel est le nouvel état de la file ?)
5. Types Abstraits et Implémentation : Les Idées Géniales derrière le Code ! 🧠
Tu sais, les listes chaînées, les listes (abstraites), les piles et les files dont on vient de parler… Ce sont des concepts, des « idées » ! Dans le monde de l’informatique, on appelle ça des Types Abstraits de Données (ou TAD pour les intimes). C’est comme le plan d’une super voiture : on sait ce qu’elle doit faire (rouler, freiner, etc.) et comment on doit interagir avec elle (volant, pédales), mais on ne sait pas encore comment elle est construite sous le capot (moteur, roues, etc.).
L’avantage des TAD, c’est qu’ils nous permettent de réfléchir aux problèmes sans nous soucier des détails techniques du langage de programmation. C’est de la « haute voltige » de la pensée algorithmique !
Mais pour que ton ordinateur (qui est un peu bête, il faut lui tout lui expliquer !) puisse utiliser ces idées, il faut les implémenter. C’est-à-dire, les « traduire » dans un langage de programmation spécifique (Python, Java, C#, etc.).
Comment on implémente ces idées ? Les outils du magicien ! 🛠️
Pour construire nos TAD, les langages de programmation utilisent souvent deux structures concrètes :
- Les Tableaux (ou Arrays) : La Commode à Tiroirs ! 🗄️ Imagine une commode avec des tiroirs numérotés qui se suivent parfaitement en mémoire. Chaque tiroir a une adresse précise, juste après le précédent.![Schéma d’un tableau en mémoire, montrant des cases contiguës numérotées (adresses mémoire) remplies de valeurs.]Le hic ? La taille d’une commode classique est fixe. Si tu veux ajouter un tiroir au milieu, tu dois acheter une nouvelle commode plus grande et tout déménager ! C’est un peu lourd. Heureusement, Python a une version « super-héro » des tableaux : les tableaux dynamiques (ce que Python appelle simplement « listes »). Ces « listes Python » sont géniales parce qu’elles gèrent automatiquement le déménagement pour toi quand tu ajoutes ou retires des éléments. C’est pour ça qu’elles sont très souvent utilisées pour implémenter nos TAD (listes, piles, files) ! Attention : Ne confonds pas les « listes Python » avec le concept abstrait de « liste » que nous avons vu au début. Ce sont des « faux amis » ! Une liste Python est un tableau dynamique !!
- * Les Listes Chaînées : La Chasse au Trésor (revisité) ! 🗺️ Comme nous l’avons vu au début, la liste chaînée est elle-même une structure d’implémentation très courante pour les TAD comme les listes (abstraites), les piles et les files. Leur flexibilité à l’insertion et suppression les rend idéales pour ces rôles.
Python te donne même la liberté d’implémenter ces TAD avec d’autres structures, comme les tuples (qui sont immuables, une propriété sympa pour la programmation fonctionnelle !).
À faire vous-même 4 : Le Dissecteur de Code Python 🐍🔬
Nous allons maintenant voir une implémentation du TAD « Liste » en Python, en utilisant des tuples (qui sont immuables !). C’est une façon très « fonctionnelle » de faire les choses, car chaque opération qui « modifie » la liste en réalité retourne une nouvelle liste (un nouveau tuple).
Étudie attentivement les fonctions suivantes et essaie de comprendre comment elles recréent le comportement de nos sorts magiques de liste :
Python
def vide():
return None # Une liste vide est représentée par None
def construire_liste(x, L): # C'est notre 'cons' !
return (x, L) # Un tuple (élément, reste_de_la_liste)
def ajouter_en_tete(L, x): # Attention, l'ordre des arguments est inversé ici par rapport au texte !
return construire_liste(x, L) # Crée une NOUVELLE liste avec x en tête
def supprimer_en_tete(L):
# Renvoie la tête (L[0]) et la queue (L[1])
# Attention: cette fonction suppose que la liste n'est PAS vide.
# Dans une vraie implémentation, on ajouterait une vérification.
return (L[0], L[1])
def est_vide(L):
return L is None # Une liste est vide si elle est None
def compter_elements(L):
if est_vide(L):
return 0
return 1 + compter_elements(L[1]) # Appel récursif sur la queue de la liste
À faire vous-même 5 : L’Expérience en Console ! 🧪
Saisis les fonctions de l’exercice « À faire vous-même 4 » dans une console Python (ou un fichier .py que tu exécutes). Puis, tape successivement ces commandes et observe attentivement ce qui se passe à chaque étape :
Python
L = vide()
print(f"L est vide : {est_vide(L)}")
L = construire_liste(5, construire_liste(4, construire_liste(3, construire_liste(2, construire_liste(1, construire_liste(0,L))))))
print(f"L après construction : {L}")
print(f"L est vide : {est_vide(L)}")
print(f"Nombre d'éléments dans L : {compter_elements(L)}")
L = ajouter_en_tete(L, 6) # Attention à l'ordre des arguments L et x ici !
print(f"L après ajout de 6 : {L}")
print(f"Nombre d'éléments dans L : {compter_elements(L)}")
x, L = supprimer_en_tete(L)
print(f"Élément supprimé (x) : {x}")
print(f"L après suppression : {L}")
print(f"Nombre d'éléments dans L : {compter_elements(L)}")
x, L = supprimer_en_tete(L)
print(f"Élément supprimé (x) : {x}")
print(f"L après 2ème suppression : {L}")
print(f"Nombre d'éléments dans L : {compter_elements(L)}")
Exercices d’application
Exercice 1 : Créer une Séquence Numérique en Liste
Énoncé
Écris une fonction creer_liste_numerique(n) qui prend en argument un entier n, supposé positif ou nul, et renvoie une liste (au sens de notre TAD avec construire_liste) contenant les entiers de 1 à n dans l’ordre croissant. Si n est 0, la liste renvoyée doit être vide.
Prérequis
- Avoir bien compris le concept de liste abstraite et l’opération
construire_liste(oucons). - Savoir gérer les cas de base dans les fonctions récursives (ici,
n = 0).
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L): # C'est notre 'cons' !
return (x, L)
# --- Fonction à écrire pour l'exercice ---
def creer_liste_numerique(n):
"""
Renvoie une liste (TAD) contenant les entiers de 1 à n.
Args:
n (int): Un entier positif ou nul.
Returns:
tuple or None: La liste des entiers de 1 à n.
"""
if n == 0:
return vide()
else:
# On construit la liste de manière récursive, en ajoutant les nombres
# du plus grand au plus petit pour obtenir l'ordre croissant à la fin
# (car 'construire_liste' ajoute en tête)
return construire_liste(n, creer_liste_numerique(n - 1))
# --- Tests ---
print("Exercice 1 :")
L0 = creer_liste_numerique(0)
print(f"creer_liste_numerique(0) : {L0} (vide si None)") # Attend None
L3 = creer_liste_numerique(3)
print(f"creer_liste_numerique(3) : {L3}") # Attend (3, (2, (1, None)))
L5 = creer_liste_numerique(5)
print(f"creer_liste_numerique(5) : {L5}") # Attend (5, (4, (3, (2, (1, None)))))
print("-" * 20)
Explication de la correction : La fonction creer_liste_numerique est récursive.
- Cas de base : Si
nest0, il n’y a pas d’éléments à ajouter, donc on renvoie une listevide(). - Cas récursif : Si
nest supérieur à0, on veut quensoit le premier élément de notre liste. On utilise doncconstruire_liste(n, ...)et pour le reste de la liste, on fait un appel récursif àcreer_liste_numerique(n - 1). Cet appel construira la liste des nombres de1àn-1, qui sera la queue de notre liste. Ainsi, lensera bien en tête, suivi den-1, etc., jusqu’à1.
Exercice 2 : Afficher les Éléments d’une Liste
Énoncé
Écris une fonction afficher_elements_liste(ma_liste) qui parcourt et affiche tous les éléments de la liste ma_liste, séparés par des espaces, suivis d’un retour à la ligne. Propose une version récursive et une version itérative (avec une boucle while).
Prérequis
- Maîtriser la récursion.
- Savoir manipuler les listes (TAD) avec
est_vide,supprimer_en_teteou en accédant directement àL[0](tête) etL[1](queue) si tu utilises l’implémentation par tuple.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
def supprimer_en_tete(L): # Utile pour la version itérative
return (L[0], L[1])
# --- Fonctions à écrire pour l'exercice ---
# Version récursive
def afficher_elements_liste_rec(ma_liste):
"""
Affiche récursivement les éléments d'une liste (TAD).
Args:
ma_liste (tuple or None): La liste à afficher.
"""
if not est_vide(ma_liste):
print(ma_liste[0], end=" ") # Affiche l'élément actuel
afficher_elements_liste_rec(ma_liste[1]) # Appel récursif sur la queue
else:
print() # Pour le retour à la ligne à la fin
# Version itérative (avec boucle while)
def afficher_elements_liste_iter(ma_liste):
"""
Affiche itérativement les éléments d'une liste (TAD).
Args:
ma_liste (tuple or None): La liste à afficher.
"""
temp_list = ma_liste # On utilise une variable temporaire pour ne pas modifier la liste originale
while not est_vide(temp_list):
print(temp_list[0], end=" ")
temp_list = temp_list[1] # Passe à l'élément suivant (la queue)
print() # Pour le retour à la ligne à la fin
# --- Tests ---
print("Exercice 2 :")
L_test = construire_liste(10, construire_liste(20, construire_liste(30, vide())))
print("Affichage récursif :")
afficher_elements_liste_rec(L_test) # Attend : 10 20 30
print("Affichage itératif :")
afficher_elements_liste_iter(L_test) # Attend : 10 20 30
L_vide = vide()
print("Affichage récursif liste vide :")
afficher_elements_liste_rec(L_vide) # Attend un retour à la ligne
print("Affichage itératif liste vide :")
afficher_elements_liste_iter(L_vide) # Attend un retour à la ligne
print("-" * 20)
Explication de la correction :
- Version récursive (
afficher_elements_liste_rec) :- Cas de base : Si la liste est vide (
est_vide(ma_liste)estTrue), cela signifie qu’on a parcouru tous les éléments. On imprime alors un retour à la ligne et la récursion s’arrête. - Cas récursif : Si la liste n’est pas vide, on imprime la tête de la liste (
ma_liste[0]) suivie d’un espace (end=" "). Ensuite, on fait un appel récursif sur la queue de la liste (ma_liste[1]) pour traiter les éléments restants.
- Cas de base : Si la liste est vide (
- Version itérative (
afficher_elements_liste_iter) :- On utilise une variable
temp_listpour ne pas modifier la liste originale passée en argument. - La boucle
whilecontinue tant quetemp_listn’est pas vide. - À chaque itération, on imprime la tête de
temp_listet on met à jourtemp_listpour qu’elle pointe vers sa propre queue. Cela simule le déplacement le long de la liste chaînée. - Une fois la boucle terminée (quand
temp_listestNone), on imprime un retour à la ligne.
- On utilise une variable
Exercice 3 : Accéder au N-ième Élément (Itératif)
Énoncé
Soit la fonction récursive obtenir_nieme_element :
Python
def obtenir_nieme_element_rec(n, lst):
"""
Renvoie le n-ième élément de la liste lst.
Les éléments sont numérotés à partir de 0.
Args:
n (int): L'index de l'élément à récupérer.
lst (tuple or None): La liste.
Raises:
IndexError: Si l'indice est invalide (liste trop courte ou liste vide initialement).
Returns:
Any: L'élément à l'indice n.
"""
if lst is None:
raise IndexError("Indice invalide : la liste est vide ou l'indice est hors limites.")
if n == 0:
return lst[0] # Accède à la tête (valeur)
else:
return obtenir_nieme_element_rec(n - 1, lst[1]) # Récursion sur la queue
Réécris cette fonction en utilisant une boucle while.
Prérequis
- Maîtriser les boucles
while. - Comprendre comment parcourir une liste chaînée étape par étape.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# --- Fonction à écrire pour l'exercice ---
def obtenir_nieme_element_iter(n, lst):
"""
Renvoie le n-ième élément de la liste lst en utilisant une boucle while.
Les éléments sont numérotés à partir de 0.
Args:
n (int): L'index de l'élément à récupérer.
lst (tuple or None): La liste.
Raises:
IndexError: Si l'indice est invalide (liste trop courte ou liste vide initialement).
Returns:
Any: L'élément à l'indice n.
"""
if n < 0:
raise IndexError("L'indice ne peut pas être négatif.")
current_list = lst
current_index = 0
while not est_vide(current_list):
if current_index == n:
return current_list[0] # On a trouvé l'élément !
current_list = current_list[1] # Passe à l'élément suivant (la queue)
current_index += 1
# Si la boucle se termine, c'est que l'indice est trop grand ou la liste était vide
raise IndexError("Indice invalide : la liste est trop courte ou l'indice est hors limites.")
# --- Tests ---
print("Exercice 3 :")
L_test = construire_liste('A', construire_liste('B', construire_liste('C', vide())))
print(f"Liste de test : {L_test}")
print(f"Élément à l'index 0 : {obtenir_nieme_element_iter(0, L_test)}") # Attend 'A'
print(f"Élément à l'index 1 : {obtenir_nieme_element_iter(1, L_test)}") # Attend 'B'
print(f"Élément à l'index 2 : {obtenir_nieme_element_iter(2, L_test)}") # Attend 'C'
try:
print(f"Élément à l'index 3 : {obtenir_nieme_element_iter(3, L_test)}")
except IndexError as e:
print(f"Erreur attendue : {e}")
try:
print(f"Élément à l'index 0 (liste vide) : {obtenir_nieme_element_iter(0, vide())}")
except IndexError as e:
print(f"Erreur attendue : {e}")
try:
print(f"Élément à l'index -1 : {obtenir_nieme_element_iter(-1, L_test)}")
except IndexError as e:
print(f"Erreur attendue : {e}")
print("-" * 20)
Explication de la correction :
- On initialise une variable
current_listà la liste d’origine et uncurrent_indexà0. - La boucle
whilecontinue tant quecurrent_listn’est pas vide. - À chaque itération :
- On vérifie si
current_indexest égal àn. Si oui, on a trouvé l’élément et on le renvoie (current_list[0]). - Si non, on « avance » dans la liste en faisant pointer
current_listvers sa queue (current_list[1]) et on incrémentecurrent_index.
- On vérifie si
- Si la boucle se termine sans avoir trouvé l’élément (c’est-à-dire que
current_listest devenueNoneavant quecurrent_indexn’atteignen), cela signifie que l’indicenest hors des limites de la liste. On lève alors uneIndexError. - On ajoute une vérification pour les indices négatifs en début de fonction.
Exercice 4 : Compter les Occurrences
Énoncé
Écris une fonction compter_occurrences(valeur, ma_liste) qui renvoie le nombre de fois où valeur apparaît dans ma_liste. Propose une version récursive et une version itérative (avec une boucle while).
Prérequis
- Maîtriser la récursion.
- Savoir parcourir une liste chaînée.
- Connaître l’opérateur d’égalité
==.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# --- Fonctions à écrire pour l'exercice ---
# Version récursive
def compter_occurrences_rec(valeur, ma_liste):
"""
Compte récursivement le nombre d'occurrences d'une valeur dans une liste (TAD).
Args:
valeur (Any): La valeur à chercher.
ma_liste (tuple or None): La liste où chercher.
Returns:
int: Le nombre d'occurrences.
"""
if est_vide(ma_liste):
return 0 # Si la liste est vide, il n'y a pas d'occurrences
# Vérifie si la tête correspond à la valeur
count = 0
if ma_liste[0] == valeur:
count = 1
# Ajoute le compte de la queue de la liste
return count + compter_occurrences_rec(valeur, ma_liste[1])
# Version itérative (avec boucle while)
def compter_occurrences_iter(valeur, ma_liste):
"""
Compte itérativement le nombre d'occurrences d'une valeur dans une liste (TAD).
Args:
valeur (Any): La valeur à chercher.
ma_liste (tuple or None): La liste où chercher.
Returns:
int: Le nombre d'occurrences.
"""
count = 0
current_list = ma_liste
while not est_vide(current_list):
if current_list[0] == valeur:
count += 1
current_list = current_list[1] # Passe à l'élément suivant
return count
# --- Tests ---
print("Exercice 4 :")
L_test = construire_liste(1, construire_liste(2, construire_liste(1, construire_liste(3, construire_liste(1, vide())))))
print(f"Liste de test : {L_test}")
print(f"Occurrences de 1 (récursif) : {compter_occurrences_rec(1, L_test)}") # Attend 3
print(f"Occurrences de 2 (récursif) : {compter_occurrences_rec(2, L_test)}") # Attend 1
print(f"Occurrences de 4 (récursif) : {compter_occurrences_rec(4, L_test)}") # Attend 0
print(f"Occurrences de 1 (itératif) : {compter_occurrences_iter(1, L_test)}") # Attend 3
print(f"Occurrences de 2 (itératif) : {compter_occurrences_iter(2, L_test)}") # Attend 1
print(f"Occurrences de 4 (itératif) : {compter_occurrences_iter(4, L_test)}") # Attend 0
print(f"Occurrences dans liste vide : {compter_occurrences_rec(5, vide())}") # Attend 0
print("-" * 20)
Explication de la correction :
- Version récursive (
compter_occurrences_rec) :- Cas de base : Si la liste est vide, il n’y a pas d’occurrences, on renvoie
0. - Cas récursif : On initialise
countà0ou1selon si la tête de la liste correspond àvaleur. Puis, on ajoute le résultat de l’appel récursif sur la queue de la liste. C’est le principe « diviser pour régner » : le problème est résolu en combinant la solution pour la tête et la solution pour le reste de la liste.
- Cas de base : Si la liste est vide, il n’y a pas d’occurrences, on renvoie
- Version itérative (
compter_occurrences_iter) :- On initialise un
countà0. - On parcourt la liste avec une boucle
whiletant qu’elle n’est pas vide. - À chaque élément, on vérifie si sa valeur (
current_list[0]) est égale àvaleur. Si oui, on incrémentecount. - On passe à l’élément suivant (
current_list = current_list[1]). - Finalement, on renvoie le
count.
- On initialise un
Exercice 5 : Trouver la Première Occurrence
Énoncé
Écris une fonction trouver_rang(valeur, ma_liste) qui renvoie le rang (l’index) de la première occurrence de valeur dans ma_liste. Si valeur n’est pas trouvée, la fonction renvoie None. Les rangs commencent à 0. Propose une version récursive et une version itérative (avec une boucle while).
Prérequis
- Maîtriser la récursion.
- Savoir parcourir une liste chaînée en gardant la trace de l’index.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# --- Fonctions à écrire pour l'exercice ---
# Version récursive (fonction auxiliaire nécessaire pour gérer l'index)
def trouver_rang_rec(valeur, ma_liste):
"""
Renvoie récursivement le rang de la première occurrence d'une valeur.
Args:
valeur (Any): La valeur à chercher.
ma_liste (tuple or None): La liste où chercher.
Returns:
int or None: Le rang de la première occurrence ou None si non trouvé.
"""
def _trouver_rang_aux(valeur, current_list, current_index):
if est_vide(current_list):
return None # Si on arrive à la fin de la liste, la valeur n'est pas trouvée
if current_list[0] == valeur:
return current_index # Si la tête correspond, on renvoie l'index actuel
# Sinon, on cherche dans la queue avec l'index incrémenté
return _trouver_rang_aux(valeur, current_list[1], current_index + 1)
return _trouver_rang_aux(valeur, ma_liste, 0) # Appel initial avec index 0
# Version itérative (avec boucle while)
def trouver_rang_iter(valeur, ma_liste):
"""
Renvoie itérativement le rang de la première occurrence d'une valeur.
Args:
valeur (Any): La valeur à chercher.
ma_liste (tuple or None): La liste où chercher.
Returns:
int or None: Le rang de la première occurrence ou None si non trouvé.
"""
current_list = ma_liste
current_index = 0
while not est_vide(current_list):
if current_list[0] == valeur:
return current_index # On a trouvé, on renvoie l'index
current_list = current_list[1] # Passe à l'élément suivant
current_index += 1
return None # Si la boucle se termine, la valeur n'a pas été trouvée
# --- Tests ---
print("Exercice 5 :")
L_test = construire_liste('pomme', construire_liste('banane', construire_liste('cerise', construire_liste('banane', vide()))))
print(f"Liste de test : {L_test}")
print(f"Rang de 'banane' (récursif) : {trouver_rang_rec('banane', L_test)}") # Attend 1
print(f"Rang de 'pomme' (récursif) : {trouver_rang_rec('pomme', L_test)}") # Attend 0
print(f"Rang de 'fraise' (récursif) : {trouver_rang_rec('fraise', L_test)}") # Attend None
print(f"Rang de 'banane' (itératif) : {trouver_rang_iter('banane', L_test)}") # Attend 1
print(f"Rang de 'pomme' (itératif) : {trouver_rang_iter('pomme', L_test)}") # Attend 0
print(f"Rang de 'fraise' (itératif) : {trouver_rang_iter('fraise', L_test)}") # Attend None
print(f"Rang dans liste vide : {trouver_rang_rec('x', vide())}") # Attend None
print("-" * 20)
Explication de la correction :
- Version récursive (
trouver_rang_rec) :- Cette version utilise une fonction auxiliaire interne (
_trouver_rang_aux) pour pouvoir passer l’index courant (current_index) dans les appels récursifs. La fonction principaletrouver_rang_recse contente d’initialiser cet index à0. - Cas de base (auxiliaire) : Si la liste est vide, cela signifie que
valeurn’a pas été trouvée, on renvoieNone. - Cas récursif (auxiliaire) : Si la tête de
current_listestvaleur, on a trouvé, on renvoiecurrent_index. Sinon, on cherche dans la queue (current_list[1]) en incrémentantcurrent_index.
- Cette version utilise une fonction auxiliaire interne (
- Version itérative (
trouver_rang_iter) :- On utilise
current_listpour parcourir la liste etcurrent_indexpour garder le compte de la position. - La boucle
whilecontinue tant quecurrent_listn’est pas vide. - À chaque pas, on vérifie si l’élément actuel correspond à
valeur. Si oui, on renvoiecurrent_indexet on sort de la fonction. - Si non, on passe à l’élément suivant et on incrémente l’index.
- Si la boucle se termine, c’est que
valeurn’a pas été trouvée, on renvoieNone.
- On utilise
Exercice 6 : Concaténation Inversée et Renversement Efficace
Énoncé
Écris une fonction récursive concatener_inverse(l1, l2) qui renvoie une nouvelle liste résultant de la concaténation de l2 à la fin de la liste l1 renversée, mais sans créer explicitement de liste inversée intermédiaire ni utiliser de fonction renverser séparée.
Ensuite, en déduis une fonction renverser_efficace(lst) qui renvoie une nouvelle liste contenant les éléments de lst dans l’ordre inverse, avec une bonne efficacité.
Prérequis
- Maîtriser la récursion.
- Comprendre l’opération
construire_listeet son effet sur l’ordre des éléments.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonctions à écrire pour l'exercice ---
def concatener_inverse(l1, l2):
"""
Renvoie une nouvelle liste qui est la concaténation de l2 à la fin de l1 inversée.
Ne crée pas l'inverse de l1 explicitement.
Args:
l1 (tuple or None): La première liste.
l2 (tuple or None): La deuxième liste.
Returns:
tuple or None: La nouvelle liste concaténée et inversée.
"""
if est_vide(l1):
return l2 # Si l1 est vide, son inverse est vide, donc on renvoie juste l2
else:
# On prend la tête de l1, et on l'ajoute à la fin de la concaténation
# inverse de la queue de l1 avec l2
# C'est magique : en "déroulant" l1, on la reconstruit à l'envers sur l2 !
return concatener_inverse(l1[1], construire_liste(l1[0], l2))
def renverser_efficace(lst):
"""
Renvoie une nouvelle liste contenant les éléments de lst dans l'ordre inverse,
en utilisant concatener_inverse pour une bonne efficacité.
Args:
lst (tuple or None): La liste à inverser.
Returns:
tuple or None: La liste inversée.
"""
return concatener_inverse(lst, vide())
# --- Tests ---
print("Exercice 6 :")
L_test1 = construire_liste(1, construire_liste(2, construire_liste(3, vide())))
L_test2 = construire_liste('A', construire_liste('B', vide()))
print(f"Liste 1 : {afficher_liste_simple(L_test1)}") # Attend (1 2 3)
print(f"Liste 2 : {afficher_liste_simple(L_test2)}") # Attend (A B)
# L1 inversée (3 2 1) + L2 (A B) => (3 2 1 A B)
res_concat_inv = concatener_inverse(L_test1, L_test2)
print(f"concatener_inverse(L1, L2) : {afficher_liste_simple(res_concat_inv)}")
# Attend : (3 2 1 A B)
res_renverser = renverser_efficace(L_test1)
print(f"renverser_efficace(L1) : {afficher_liste_simple(res_renverser)}")
# Attend : (3 2 1)
res_renverser_vide = renverser_efficace(vide())
print(f"renverser_efficace(liste_vide) : {afficher_liste_simple(res_renverser_vide)}")
# Attend : ()
print("-" * 20)
Explication de la correction :
concatener_inverse(l1, l2):- C’est une technique récursive très astucieuse !
- Cas de base : Si
l1est vide, cela signifie que tous ses éléments ont été traités et « ajoutés » àl2. Donc,l2contient maintenant tous les éléments de l1 (inversés) suivis de ses propres éléments originaux. On renvoie simplementl2. - Cas récursif : Si
l1n’est pas vide :- On prend la tête de
l1(l1[0]). - On fait un appel récursif sur la queue de
l1(l1[1]). - MAIS, au lieu de passer
l2directement, on passeconstruire_liste(l1[0], l2). Cela signifie qu’on « ajoute » la tête actuelle del1à la tête de la listel2qui sera construite dans les appels futurs. À chaque appel récursif, l’élément del1est ajouté en tête d’une liste qui grossit et qui finit par êtrel2. C’est comme si on empilait les éléments del1surl2au fur et à mesure qu’on les dépile del1, ce qui les inverse naturellement.
- On prend la tête de
renverser_efficace(lst):- Une fois
concatener_inversecomprise,renverser_efficacedevient trivial. Il suffit de concaténerlst(la liste à inverser) avec une liste vide (vide()). La fonctionconcatener_inverseva inverserlstet y ajouter la liste vide à la fin, ce qui donne exactement l’inverse delst. - Cette approche est efficace car elle ne crée pas de multiples listes intermédiaires complètes, mais construit la liste inversée « en passant ».
- Une fois
Exercice 7 : Comparer l’Identité de Deux Listes
Énoncé
Écris une fonction sont_identiques(l1, l2) qui renvoie un booléen (True ou False) indiquant si les listes l1 et l2 sont identiques. Pour être identiques, elles doivent contenir exactement les mêmes éléments, dans le même ordre. On suppose que l’on peut comparer les éléments avec l’opérateur ==. Propose une version récursive et une version itérative (avec une boucle while).
Prérequis
- Savoir manipuler les listes chaînées.
- Gérer les différents cas (listes vides, listes de tailles différentes, éléments différents).
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# --- Fonctions à écrire pour l'exercice ---
# Version récursive
def sont_identiques_rec(l1, l2):
"""
Vérifie récursivement si deux listes (TAD) sont identiques.
Args:
l1 (tuple or None): La première liste.
l2 (tuple or None): La deuxième liste.
Returns:
bool: True si les listes sont identiques, False sinon.
"""
if est_vide(l1) and est_vide(l2):
return True # Si les deux sont vides, elles sont identiques
if est_vide(l1) or est_vide(l2):
return False # Si l'une est vide et l'autre non, elles ne sont pas identiques
# Si les têtes sont différentes, les listes ne sont pas identiques
if l1[0] != l2[0]:
return False
# Si les têtes sont identiques, on compare récursivement les queues
return sont_identiques_rec(l1[1], l2[1])
# Version itérative (avec boucle while)
def sont_identiques_iter(l1, l2):
"""
Vérifie itérativement si deux listes (TAD) sont identiques.
Args:
l1 (tuple or None): La première liste.
l2 (tuple or None): La deuxième liste.
Returns:
bool: True si les listes sont identiques, False sinon.
"""
current_l1 = l1
current_l2 = l2
while not est_vide(current_l1) and not est_vide(current_l2):
if current_l1[0] != current_l2[0]:
return False # Éléments différents, donc pas identiques
current_l1 = current_l1[1]
current_l2 = current_l2[1]
# Après la boucle, les deux listes devraient être vides si elles sont identiques
return est_vide(current_l1) and est_vide(current_l2)
# --- Tests ---
print("Exercice 7 :")
L_test1 = construire_liste(1, construire_liste(2, construire_liste(3, vide())))
L_test2 = construire_liste(1, construire_liste(2, construire_liste(3, vide())))
L_test3 = construire_liste(1, construire_liste(2, construire_liste(4, vide()))) # Différent par élément
L_test4 = construire_liste(1, construire_liste(2, vide())) # Différent par taille
print(f"L1 : {afficher_liste_simple(L_test1)}")
print(f"L2 : {afficher_liste_simple(L_test2)}")
print(f"L3 : {afficher_liste_simple(L_test3)}")
print(f"L4 : {afficher_liste_simple(L_test4)}")
print(f"L1 et L2 (rec) : {sont_identiques_rec(L_test1, L_test2)}") # Attend True
print(f"L1 et L3 (rec) : {sont_identiques_rec(L_test1, L_test3)}") # Attend False
print(f"L1 et L4 (rec) : {sont_identiques_rec(L_test1, L_test4)}") # Attend False
print(f"L1 et L1 (rec) : {sont_identiques_rec(L_test1, L_test1)}") # Attend True (même référence)
print(f"Liste vide et liste vide (rec) : {sont_identiques_rec(vide(), vide())}") # Attend True
print(f"L1 et liste vide (rec) : {sont_identiques_rec(L_test1, vide())}") # Attend False
print(f"L1 et L2 (iter) : {sont_identiques_iter(L_test1, L_test2)}") # Attend True
print(f"L1 et L3 (iter) : {sont_identiques_iter(L_test1, L_test3)}") # Attend False
print(f"L1 et L4 (iter) : {sont_identiques_iter(L_test1, L_test4)}") # Attend False
print(f"Liste vide et liste vide (iter) : {sont_identiques_iter(vide(), vide())}") # Attend True
print("-" * 20)
Explication de la correction :
- Version récursive (
sont_identiques_rec) :- On gère d’abord les cas de base :
- Si les deux listes sont vides, elles sont identiques (
True). - Si l’une est vide et l’autre non, elles ne peuvent pas être identiques (
False).
- Si les deux listes sont vides, elles sont identiques (
- Ensuite, si aucune des deux n’est vide, on compare leurs têtes (
l1[0]etl2[0]). Si elles sont différentes, les listes ne sont pas identiques (False). - Si les têtes sont identiques, on fait un appel récursif pour comparer les queues des deux listes (
l1[1]etl2[1]).
- On gère d’abord les cas de base :
- Version itérative (
sont_identiques_iter) :- On utilise deux variables (
current_l1,current_l2) pour parcourir les deux listes en parallèle. - La boucle
whilecontinue tant qu’aucune des deux listes n’est vide. - À chaque pas, on compare les éléments actuels (
current_l1[0]etcurrent_l2[0]). Si une différence est trouvée, on renvoieFalseimmédiatement. - Si les éléments sont égaux, on passe aux queues des deux listes.
- Après la boucle, si les deux listes sont devenues vides en même temps (
est_vide(current_l1) and est_vide(current_l2)), c’est qu’elles étaient identiques. Sinon (si une seule est vide, ou aucune mais elles se sont arrêtées pour une autre raison – impossible ici), elles ne le sont pas.
- On utilise deux variables (
Exercice 8 : Insérer dans une Liste Triée
Énoncé
Écris une fonction récursive inserer_triee(x, lst) qui prend en arguments un entier x et une liste d’entiers lst, supposée déjà triée par ordre croissant. La fonction doit renvoyer une nouvelle liste dans laquelle x a été inséré à sa place correcte pour maintenir l’ordre trié.
Exemple : insérer la valeur 3 dans la liste (1, 2, 5, 8) renvoie la liste (1, 2, 3, 5, 8).
Prérequis
- Maîtriser la récursion.
- Comprendre comment
construire_listecrée de nouvelles listes. - Gérer les comparaisons d’éléments.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonction à écrire pour l'exercice ---
def inserer_triee(x, lst):
"""
Insère un élément x dans une liste triée (TAD) en conservant l'ordre.
Renvoie une nouvelle liste.
Args:
x (int): L'entier à insérer.
lst (tuple or None): La liste d'entiers triée.
Returns:
tuple or None: La nouvelle liste avec x inséré.
"""
if est_vide(lst):
# Si la liste est vide, on crée une liste avec juste x
return construire_liste(x, vide())
# Si x est plus petit ou égal à la tête de la liste, x est inséré ici
if x <= lst[0]:
return construire_liste(x, lst)
else:
# Sinon, x est plus grand que la tête, on cherche sa place dans la queue
# et on reconstruit la liste avec la tête actuelle.
return construire_liste(lst[0], inserer_triee(x, lst[1]))
# --- Tests ---
print("Exercice 8 :")
L_triee1 = construire_liste(1, construire_liste(2, construire_liste(5, construire_liste(8, vide()))))
print(f"Liste triée originale : {afficher_liste_simple(L_triee1)}")
res1 = inserer_triee(3, L_triee1)
print(f"Insertion de 3 : {afficher_liste_simple(res1)}") # Attend (1 2 3 5 8)
res2 = inserer_triee(0, L_triee1)
print(f"Insertion de 0 : {afficher_liste_simple(res2)}") # Attend (0 1 2 5 8)
res3 = inserer_triee(10, L_triee1)
print(f"Insertion de 10 : {afficher_liste_simple(res3)}") # Attend (1 2 5 8 10)
res4 = inserer_triee(5, L_triee1) # Insertion d'un doublon
print(f"Insertion de 5 : {afficher_liste_simple(res4)}") # Attend (1 2 5 5 8)
res5 = inserer_triee(7, vide())
print(f"Insertion dans liste vide : {afficher_liste_simple(res5)}") # Attend (7)
print("-" * 20)
Explication de la correction :
- Cas de base : Si la liste
lstest vide,xdoit être le seul élément de la nouvelle liste. On renvoie doncconstruire_liste(x, vide()). - Cas récursif :
- Si
xest plus petit ou égal à la tête de la liste actuelle (lst[0]), alorsxdoit être inséré avant cette tête. On renvoie alorsconstruire_liste(x, lst). - Sinon (si
xest plus grand quelst[0]), cela signifie quelst[0]doit rester à sa place. On fait donc un appel récursif pour insérerxdans la queue de la liste (lst[1]). Le résultat de cet appel récursif formera la nouvelle queue, à laquelle on « raccroche » la tête actuelle delst.
- Si
Exercice 9 : Tri par Insertion Récursif
Énoncé
En te servant de la fonction inserer_triee de l’exercice précédent, écris une fonction récursive tri_par_insertion(lst) qui prend en argument une liste d’entiers lst et renvoie une nouvelle liste, contenant les mêmes éléments mais triée par ordre croissant.
Prérequis
- Avoir terminé l’Exercice 8 (
inserer_triee). - Maîtriser la récursion.
- Comprendre le principe du tri par insertion : prendre un élément, l’insérer au bon endroit dans une liste déjà triée.
Proposition de correction
Python
# On réutilise les fonctions d'aide et inserer_triee
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonction de l'exercice 8
def inserer_triee(x, lst):
if est_vide(lst):
return construire_liste(x, vide())
if x <= lst[0]:
return construire_liste(x, lst)
else:
return construire_liste(lst[0], inserer_triee(x, lst[1]))
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonction à écrire pour l'exercice ---
def tri_par_insertion(lst):
"""
Trie une liste (TAD) par insertion récursive.
Renvoie une nouvelle liste triée.
Args:
lst (tuple or None): La liste à trier.
Returns:
tuple or None: La nouvelle liste triée.
"""
if est_vide(lst):
return vide() # Une liste vide est déjà triée
# On prend la tête de la liste
tête = lst[0]
# On trie récursivement la queue de la liste
queue_triee = tri_par_insertion(lst[1])
# Et on insère la tête dans la queue triée
return inserer_triee(tête, queue_triee)
# --- Tests ---
print("Exercice 9 :")
L_non_triee1 = construire_liste(5, construire_liste(2, construire_liste(8, construire_liste(1, construire_liste(3, vide())))))
print(f"Liste non triée : {afficher_liste_simple(L_non_triee1)}")
res_tri1 = tri_par_insertion(L_non_triee1)
print(f"Liste triée : {afficher_liste_simple(res_tri1)}") # Attend (1 2 3 5 8)
L_non_triee2 = construire_liste(9, construire_liste(1, construire_liste(5, vide())))
print(f"Liste non triée : {afficher_liste_simple(L_non_triee2)}")
res_tri2 = tri_par_insertion(L_non_triee2)
print(f"Liste triée : {afficher_liste_simple(res_tri2)}") # Attend (1 5 9)
res_tri_vide = tri_par_insertion(vide())
print(f"Liste vide triée : {afficher_liste_simple(res_tri_vide)}") # Attend ()
L_single = construire_liste(42, vide())
print(f"Liste à un élément triée : {afficher_liste_simple(L_single)}")
res_single = tri_par_insertion(L_single)
print(f"Résultat : {afficher_liste_simple(res_single)}") # Attend (42)
print("-" * 20)
Explication de la correction :
- Cas de base : Si la liste
lstest vide, elle est déjà triée. On renvoie une liste vide. - Cas récursif :
- On prend le premier élément de la liste (
lst[0]). C’est l’élément que nous allons insérer. - On appelle récursivement
tri_par_insertionsur le reste de la liste (lst[1]). Cet appel nous renvoie unequeue_triee(une nouvelle liste, qui est le reste de la liste d’origine, mais trié !). - Enfin, on utilise la fonction
inserer_triee(de l’Exercice 8) pour insérer latêtede la liste d’origine dans cettequeue_trieeà sa place correcte. Le principe du tri par insertion est parfaitement adapté à cette structure récursive : pour trier une liste, tu tries le « reste » de la liste, puis tu insères le premier élément à sa place dans ce « reste » déjà trié.
- On prend le premier élément de la liste (
Exercice 10 : Conversion Tableau vers Liste Chaînée
Énoncé
Écris une fonction tableau_vers_liste_chaine(tableau) qui prend en argument un tableau (une liste Python native) tableau et renvoie une liste chaînée (au sens de notre TAD avec construire_liste) contenant les éléments du tableau dans le même ordre. On suggère de l’écrire avec une boucle for ou while pour une efficacité optimale, mais une version récursive est aussi possible (un peu moins intuitive ici).
Prérequis
- Comprendre la différence entre un tableau Python (liste native) et notre TAD « liste chaînée ».
- Savoir parcourir un tableau Python.
- Savoir construire une liste chaînée.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonction à écrire pour l'exercice ---
# Version itérative (la plus commune et souvent la plus efficace ici)
def tableau_vers_liste_chaine(tableau):
"""
Convertit un tableau Python en une liste chaînée (TAD).
Args:
tableau (list): Le tableau Python.
Returns:
tuple or None: La liste chaînée correspondante.
"""
resultat_liste = vide()
# On parcourt le tableau EN REVERS pour pouvoir utiliser construire_liste (ajouter en tête)
for element in reversed(tableau):
resultat_liste = construire_liste(element, resultat_liste)
return resultat_liste
# Une version alternative itérative sans reversed (un peu plus complexe car nécessite de gérer le "suivant")
# def tableau_vers_liste_chaine_alt(tableau):
# if not tableau:
# return vide()
#
# head_node = construire_liste(tableau[0], vide())
# current_node = head_node
#
# for i in range(1, len(tableau)):
# # Ici, on devrait créer un nouveau nœud et l'attacher à current_node[1]
# # Mais avec notre implémentation de tuple, c'est pas direct car les tuples sont immuables.
# # Cette approche serait plus naturelle avec une implémentation de liste chaînée mutable (avec des classes).
# pass # C'est pourquoi la version reversed est privilégiée ici.
# Version récursive (moins intuitive pour cette tâche)
def tableau_vers_liste_chaine_rec(tableau):
"""
Convertit récursivement un tableau Python en une liste chaînée (TAD).
Args:
tableau (list): Le tableau Python.
Returns:
tuple or None: La liste chaînée correspondante.
"""
if not tableau:
return vide()
# On prend le premier élément du tableau et on le construit sur le reste
# qui est la conversion récursive du reste du tableau.
return construire_liste(tableau[0], tableau_vers_liste_chaine_rec(tableau[1:]))
# --- Tests ---
print("Exercice 10 :")
tab1 = [10, 20, 30, 40]
res_liste1 = tableau_vers_liste_chaine(tab1)
print(f"Tableau {tab1} -> Liste Chaînée : {afficher_liste_simple(res_liste1)}") # Attend (10 20 30 40)
tab2 = ['a', 'b']
res_liste2 = tableau_vers_liste_chaine(tab2)
print(f"Tableau {tab2} -> Liste Chaînée : {afficher_liste_simple(res_liste2)}") # Attend (a b)
tab3 = []
res_liste3 = tableau_vers_liste_chaine(tab3)
print(f"Tableau {tab3} -> Liste Chaînée : {afficher_liste_simple(res_liste3)}") # Attend ()
print("--- Version Récursive ---")
res_liste1_rec = tableau_vers_liste_chaine_rec(tab1)
print(f"Tableau {tab1} -> Liste Chaînée (réc) : {afficher_liste_simple(res_liste1_rec)}")
res_liste3_rec = tableau_vers_liste_chaine_rec(tab3)
print(f"Tableau {tab3} -> Liste Chaînée (réc) : {afficher_liste_simple(res_liste3_rec)}")
print("-" * 20)
Explication de la correction :
- Version itérative (
tableau_vers_liste_chaine) :- La clé ici est d’utiliser
reversed(tableau). Pourquoi ? Parce que notre fonctionconstruire_listeajoute toujours un élément en tête de la liste existante. Si on parcourt le tableau normalement, on construirait la liste à l’envers. En parcourant le tableau à l’envers, on ajoute le dernier élément en premier, puis l’avant-dernier qui devient la nouvelle tête, et ainsi de suite. Au final, la liste est construite dans le bon ordre. - On initialise
resultat_listeà vide, puis on ajoute les éléments un par un.
- La clé ici est d’utiliser
- Version récursive (
tableau_vers_liste_chaine_rec) :- Cas de base : Si le tableau est vide, on renvoie une liste vide.
- Cas récursif : On prend le premier élément du tableau (
tableau[0]) et on l’ajoute en tête d’une liste qui est le résultat de l’appel récursif sur le reste du tableau (tableau[1:]).tableau[1:]crée une copie du reste du tableau, ce qui peut être moins performant pour de très grands tableaux mais est très lisible.
Exercice 11 : Trouver la Dernière Cellule (Implémentation Chaînée)
Énoncé
Écris une fonction obtenir_derniere_cellule(lst) qui renvoie la dernière cellule (le dernier tuple (valeur, None)) de la liste chaînée lst. On suppose que la liste lst n’est pas vide.
Prérequis
- Comprendre l’implémentation de la liste chaînée avec des tuples
(valeur, suivant). - Savoir qu’une cellule est le tuple entier.
- Savoir qu’une cellule
(valeur, None)est la dernière.
Proposition de correction
Python
# On réutilise notre implémentation de liste basée sur des tuples
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonction à écrire pour l'exercice ---
def obtenir_derniere_cellule(lst):
"""
Renvoie la dernière cellule (tuple) d'une liste chaînée non vide.
Args:
lst (tuple): La liste chaînée (non vide).
Returns:
tuple: La dernière cellule de la liste.
"""
if est_vide(lst):
# Cette condition ne devrait normalement pas être atteinte d'après l'énoncé,
# mais c'est une bonne pratique de la gérer.
raise ValueError("La liste ne doit pas être vide pour cette opération.")
current_cell = lst
# On parcourt tant que la "queue" de la cellule actuelle n'est pas vide (None)
while not est_vide(current_cell[1]):
current_cell = current_cell[1] # On passe à la cellule suivante
return current_cell # Quand la boucle s'arrête, current_cell est la dernière
# --- Tests ---
print("Exercice 11 :")
L_test = construire_liste(1, construire_liste(2, construire_liste(3, vide())))
print(f"Liste de test : {afficher_liste_simple(L_test)}")
derniere = obtenir_derniere_cellule(L_test)
print(f"Dernière cellule de (1 2 3) : {derniere}") # Attend (3, None)
L_single = construire_liste(42, vide())
print(f"Liste à un élément : {afficher_liste_simple(L_single)}")
derniere_single = obtenir_derniere_cellule(L_single)
print(f"Dernière cellule de (42) : {derniere_single}") # Attend (42, None)
# Test du cas d'erreur (si l'énoncé n'avait pas garanti non vide)
try:
obtenir_derniere_cellule(vide())
except ValueError as e:
print(f"Erreur attendue sur liste vide : {e}")
print("-" * 20)
Explication de la correction :
- On initialise
current_cellavec le début de la liste (lst). - La boucle
whilecontinue tant que la queue de lacurrent_celln’est pas vide (current_cell[1]n’est pasNone). - À chaque itération, on fait avancer
current_cellà la cellule suivante (current_cell = current_cell[1]). - Lorsque la boucle se termine, cela signifie que
current_cell[1]estNone, ce qui veut dire quecurrent_cellest la dernière cellule de la liste. On la retourne. - J’ai ajouté une gestion d’erreur pour le cas où la liste serait vide, même si l’énoncé supposait qu’elle ne l’était pas.
Exercice 12 : Concaténation « En Place » (avec notre TAD)
Énoncé
En utilisant la fonction obtenir_derniere_cellule de l’exercice précédent, écris une fonction concatener_en_place_simule(l1, l2) qui réalise une concaténation « en place » des listes l1 et l2. Cela signifie que la fonction doit « relier » la dernière cellule de l1 à la première cellule de l2. Cette fonction doit renvoyer la toute première cellule de la concaténation (l1 si l1 n’est pas vide, sinon l2).
Attention : Avec notre implémentation de listes basée sur des tuples, une vraie « modification en place » est impossible car les tuples sont immuables. Nous allons donc simuler cette opération en créant de nouveaux tuples pour représenter la nouvelle structure, mais en conservant l’idée de « lier » la fin de l1 au début de l2. Cette fonction sera donc plus complexe qu’avec une vraie liste chaînée mutable.
Alternativement, tu peux simplifier la simulation en considérant que l1 doit être reconstruite depuis le début si elle n’est pas vide, pour que son dernier élément pointe vers l2.
Prérequis
- Avoir terminé l’Exercice 11 (
obtenir_derniere_cellule). - Comprendre le concept d’immuabilité des tuples en Python et l’impact sur la « modification en place ».
- Maîtriser la récursion pour la reconstruction.
Proposition de correction
Note sur l’immuabilité : L’énoncé original de l’exercice 59 sur pixees.fr est conçu pour des implémentations de listes chaînées mutables (où on peut modifier la partie suivant d’un nœud existant). Notre implémentation avec des tuples (valeur, suivant) est immuable. Cela signifie que (3, None) ne peut jamais devenir (3, (4, None)). Pour « modifier » la liste, nous devons toujours créer de nouvelles parties de la liste.
Il y a deux façons de l’aborder avec notre TAD immuable :
- Approche « purement fonctionnelle » (reconstruction) : La plus idiomatique avec des tuples. On reconstruit
l1en changeant le pointeurNonede sa dernière cellule pour qu’il pointe versl2. - Approche « simplifiée » (pour coller à l’esprit de l’exercice original, mais qui n’est pas une vraie « modification en place ») : Si
l1est vide, le résultat estl2. Sil1n’est pas vide, on inversel1(pour pouvoir la parcourir facilement), puis on la concatène avecl2. Cette approche perd l’aspect « en place » mais utilise les primitives.
Je vais te proposer la première approche, qui est plus fidèle à la nature immuable de nos tuples et qui montre la complexité de simuler l’en-place avec des immuables. C’est un excellent point de discussion sur les Trade-offs !
Python
# On réutilise nos fonctions d'aide
def vide():
return None
def construire_liste(x, L):
return (x, L)
def est_vide(L):
return L is None
# Fonction de l'exercice 11
def obtenir_derniere_cellule(lst):
if est_vide(lst):
raise ValueError("La liste ne doit pas être vide pour cette opération.")
current_cell = lst
while not est_vide(current_cell[1]):
current_cell = current_cell[1]
return current_cell
# Fonctions d'affichage pour les tests
def afficher_liste_simple(ma_liste):
elements = []
current = ma_liste
while not est_vide(current):
elements.append(str(current[0]))
current = current[1]
return "(" + " ".join(elements) + ")"
# --- Fonction à écrire pour l'exercice (Simulation "en place" par reconstruction) ---
# Fonction auxiliaire pour copier une liste jusqu'à un certain point
def _copier_jusqu_a_element(liste, element_cible, nouvelle_fin):
"""
Copie la liste 'liste' jusqu'à l'élément 'element_cible' et attache 'nouvelle_fin' à ce point.
Cette fonction est récursive et gère la reconstruction de la liste IMMUABLE.
"""
if est_vide(liste):
# Ne devrait pas arriver si element_cible est dans la liste
return vide()
# Si on arrive à l'élément cible (la dernière cellule de l1), on change son pointeur
if liste == element_cible: # Comparaison par identité (même tuple)
return construire_liste(liste[0], nouvelle_fin)
# Sinon, on copie la tête et on continue la récursion sur la queue
return construire_liste(liste[0], _copier_jusqu_a_element(liste[1], element_cible, nouvelle_fin))
def concatener_en_place_simule(l1, l2):
"""
Simule une concaténation "en place" de l1 et l2 pour des listes immuables.
Args:
l1 (tuple or None): La première liste.
l2 (tuple or None): La deuxième liste.
Returns:
tuple or None: La nouvelle liste résultante (début de l1 ou l2).
"""
if est_vide(l1):
return l2 # Si l1 est vide, le résultat est simplement l2
if est_vide(l2):
return l1 # Si l2 est vide, le résultat est simplement l1
# On trouve la dernière "cellule" de l1
derniere_cell_l1 = obtenir_derniere_cellule(l1)
# Avec des listes immuables (tuples), on ne peut pas faire :
# derniere_cell_l1[1] = l2 (ça ne marcherait pas car les tuples ne sont pas mutables)
# On doit donc reconstruire l1 en changeant le pointeur de sa dernière cellule.
# C'est ici que l'approche "en place" perd de son sens avec des immuables.
# On va reconstruire l1 jusqu'à la dernière cellule, puis la faire pointer vers l2.
# Utilisons la fonction auxiliaire pour "reconstruire" l1 avec le nouveau lien
# C'est une "modification" qui crée une nouvelle version de l1
nouvelle_l1 = _copier_jusqu_a_element(l1, derniere_cell_l1, l2)
return nouvelle_l1 # Le début de la concaténation est le début de la nouvelle l1
# --- Tests ---
print("Exercice 12 :")
L_a = construire_liste(1, construire_liste(2, vide()))
L_b = construire_liste('A', construire_liste('B', vide()))
print(f"L_a originale : {afficher_liste_simple(L_a)}")
print(f"L_b originale : {afficher_liste_simple(L_b)}")
# Tentative de concaténation "en place"
L_concat = concatener_en_place_simule(L_a, L_b)
print(f"L_a après simulation : {afficher_liste_simple(L_a)}") # L_a devrait rester inchangée si l'implémentation est immuable
print(f"L_concat (résultat) : {afficher_liste_simple(L_concat)}") # Attend (1 2 A B)
# Test avec L_a vide
L_vide = vide()
L_concat_vide_debut = concatener_en_place_simule(L_vide, L_b)
print(f"L_concat (vide + L_b) : {afficher_liste_simple(L_concat_vide_debut)}") # Attend (A B)
# Test avec L_b vide
L_concat_vide_fin = concatener_en_place_simule(L_a, L_vide)
print(f"L_concat (L_a + vide) : {afficher_liste_simple(L_concat_vide_fin)}") # Attend (1 2)
# Test avec les deux vides
L_concat_deux_vides = concatener_en_place_simule(L_vide, L_vide)
print(f"L_concat (vide + vide) : {afficher_liste_simple(L_concat_deux_vides)}") # Attend ()
print("-" * 20)
Explication de la correction :
C’est l’exercice le plus délicat avec notre implémentation par tuples car les tuples sont immuables. On ne peut pas simplement dire ma_cellule[1] = nouvelle_valeur si ma_cellule est un tuple. Cela lèverait une erreur.
- Gestion des cas limites : Si
l1est vide, la concaténation donnel2. Sil2est vide, elle donnel1. C’est simple et direct. - Trouver la dernière cellule de
l1: On utiliseobtenir_derniere_cellule(l1). Cela nous donne la référence au tuple qui est le dernier élément del1. - La « simulation » de la modification : Puisque nous ne pouvons pas modifier le tuple
derniere_cell_l1en changeant sa partie[1](suivant), nous devons reconstruire la partie del1qui mène à cette dernière cellule, en faisant en sorte que la nouvelle version de cette dernière cellule pointe versl2.- La fonction auxiliaire
_copier_jusqu_a_elementparcourtl1récursivement. Quand elle atteint lederniere_cell_l1(comparaison par identité pour s’assurer que c’est bien la même référence au tuple), elle crée un nouveau tuple pour cette dernière cellule, avec sa valeur originale et en le faisant pointer versl2au lieu deNone. - Les appels récursifs précédents de
_copier_jusqu_a_element« raccrochent » ensuite les éléments précédents del1à cette nouvelle structure, recréant une « nouvelle version » del1qui al2attachée à sa fin.
- La fonction auxiliaire
- Retour : La fonction renvoie le début de cette
nouvelle_l1.
Cette implémentation met en lumière pourquoi les listes chaînées « en place » sont souvent implémentées avec des objets mutables (classes en Python, structs en C) où les attributs valeur et suivant peuvent être directement modifiés, sans avoir à reconstruire toute une portion de la liste. C’est un excellent exemple des compromis liés aux choix d’implémentation !
Exercices : Les Piles et Files, C’est de la Bombe ! 💥
Ces exercices vont te propulser au niveau supérieur. Nous allons cette fois travailler avec des implémentations de piles et files basées sur des classes Python, ce qui se rapproche de la réalité du code. Prépare-toi à coder !
Exercice 13 : Compléter la Classe Pile
Énoncé
On te fournit le squelette d’une classe Pile utilisant une liste chaînée (implémentée avec la classe Cellule).
Python
class Cellule:
"""une cellule d’une liste chaînée"""
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
"""structure de pile"""
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def creer_pile():
return Pile()
Complète la classe Pile avec les trois méthodes additionnelles suivantes :
consulter(self): Renvoie l’élément au sommet de la pile sans le retirer. Lève uneIndexErrorsi la pile est vide.vider(self): Vide complètement la pile.taille(self): Renvoie le nombre d’éléments dans la pile.
Quel est l’ordre de grandeur du nombre d’opérations effectuées par la fonction taille ? Exprime-le en notation Grand O (O-notation).
Prérequis
- Comprendre le fonctionnement des classes et objets en Python.
- Savoir manipuler les listes chaînées (ici via les objets
Cellule). - Connaître le principe LIFO des piles.
- Avoir une petite idée de la complexité algorithmique (O-notation).
Proposition de correction
Python
class Cellule:
"""une cellule d’une liste chaînée"""
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
"""structure de pile"""
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
# --- Nouvelles méthodes à compléter ---
def consulter(self):
"""
Renvoie l'élément au sommet de la pile sans le retirer.
Lève une IndexError si la pile est vide.
"""
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur # On accède juste à la valeur de la cellule de tête
def vider(self):
"""
Vide complètement la pile.
"""
self.contenu = None # La magie opère : il suffit de "lâcher" la référence à la première cellule !
# Le ramasse-miettes de Python fera le reste.
def taille(self):
"""
Renvoie le nombre d'éléments dans la pile.
"""
compteur = 0
courant = self.contenu # On part de la première cellule
while courant is not None:
compteur += 1
courant = courant.suivante # On avance à la cellule suivante
return compteur
def creer_pile():
return Pile()
# --- Tests ---
print("Exercice 13 : Compléter la Classe Pile")
ma_pile = creer_pile()
print(f"Pile est vide ? {ma_pile.est_vide()}") # Attend True
ma_pile.empiler(10)
ma_pile.empiler(20)
ma_pile.empiler(30)
print(f"Pile après empilement : {ma_pile.consulter()} au sommet") # Attend 30
print(f"Taille de la pile : {ma_pile.taille()}") # Attend 3
print(f"Élément consulté : {ma_pile.consulter()}") # Attend 30 (et la pile n'est pas modifiée)
print(f"Élément dépilé : {ma_pile.depiler()}") # Attend 30
print(f"Pile après dépilement : {ma_pile.consulter()} au sommet") # Attend 20
print(f"Taille de la pile : {ma_pile.taille()}") # Attend 2
ma_pile.vider()
print(f"Pile est vide après vider ? {ma_pile.est_vide()}") # Attend True
print(f"Taille de la pile après vider : {ma_pile.taille()}") # Attend 0
# Test d'erreur pour consulter et depiler sur pile vide
try:
ma_pile.consulter()
except IndexError as e:
print(f"Erreur attendue : {e}")
try:
ma_pile.depiler()
except IndexError as e:
print(f"Erreur attendue : {e}")
print("-" * 20)
Ordre de grandeur de la fonction taille :
Pour calculer la taille de la pile, la fonction taille doit parcourir toutes les cellules de la pile, de la première à la dernière. Si la pile contient N éléments, elle effectuera N opérations (un accès à suivante et une incrémentation de compteur pour chaque élément).
L’ordre de grandeur est donc mathcalO(N) (linéaire). Plus la pile est grande, plus le temps de calcul de sa taille augmente proportionnellement. Ce n’est pas la fin du monde pour les petites piles, mais pour les géantes, ça peut devenir un facteur limitant !
Exercice 14 : Navigateur Web avec Historique « Retour Avant »
Énoncé
Voici un programme qui simule une navigation web simplifiée avec une fonction « retour » :
Python
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
# ... (code de la classe Pile de l'exercice 13, y compris est_vide, empiler, depiler)
# Pour cet exercice, nous aurons besoin de consulter() et est_vide()
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def consulter(self): # Ajoutée pour cet exercice
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur
adresse_courante = ""
adresses_precedentes = Pile()
def aller_a(adresse_cible):
global adresse_courante
global adresses_suivantes # On anticipe l'ajout de cette pile
if adresse_courante: # N'empile que si on vient d'une page existante
adresses_precedentes.empiler(adresse_courante)
adresse_courante = adresse_cible
adresses_suivantes.vider() # Toute nouvelle navigation annule l'historique "avant"
def retour():
global adresse_courante
global adresses_suivantes # On en aura besoin ici
if not adresses_precedentes.est_vide():
# Avant de partir de l'adresse courante, on l'empile dans adresses_suivantes
if adresse_courante: # S'il y a une adresse courante à enregistrer
adresses_suivantes.empiler(adresse_courante)
adresse_courante = adresses_precedentes.depiler()
else:
print("Plus d'adresses précédentes. Impossible de revenir plus loin.")
# On pourrait choisir de ne rien faire ou de vider adresse_courante si on veut
# adresse_courante = "" # Optionnel : vider l'adresse courante si on est au début
On souhaite compléter ce programme pour avoir également une fonction retour_avant dont le comportement est le suivant :
- Chaque appel à la fonction
retourplace la page quittée au sommet d’une deuxième pileadresses_suivantes. - Un appel à la fonction
retour_avantamène à la page enregistrée au sommet de la pileadresses_suivantes, et met à jour les deux piles de manière adaptée. - Toute nouvelle navigation avec
aller_aannule lesadresses_suivantes.
Modifie et complète le programme pour définir cette nouvelle fonction.
Prérequis
- Maîtriser le concept de pile.
- Comprendre les interactions entre plusieurs piles pour gérer un historique.
- Gérer les variables globales en Python.
Proposition de correction
Python
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def consulter(self):
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur
def vider(self): # On a besoin de vider pour cet exercice
self.contenu = None
# --- Variables globales du simulateur de navigateur ---
adresse_courante = ""
adresses_precedentes = Pile()
adresses_suivantes = Pile() # La nouvelle pile pour l'historique "retour avant"
def aller_a(adresse_cible):
"""
Simule la navigation vers une nouvelle adresse.
Empile l'adresse courante dans les adresses précédentes et vide les adresses suivantes.
"""
global adresse_courante
global adresses_precedentes
global adresses_suivantes
if adresse_courante: # N'empile que si on vient d'une page existante (pas le premier aller_a)
adresses_precedentes.empiler(adresse_courante)
adresse_courante = adresse_cible
adresses_suivantes.vider() # Toute nouvelle navigation annule l'historique "retour avant"
print(f"-> Navigué vers : {adresse_courante}")
def retour():
"""
Revient à l'adresse précédente.
Place la page actuelle dans adresses_suivantes avant de revenir.
"""
global adresse_courante
global adresses_precedentes
global adresses_suivantes
if not adresses_precedentes.est_vide():
# Avant de changer l'adresse courante, on l'empile pour pouvoir y revenir avec retour_avant
if adresse_courante: # S'il y a bien une page courante à quitter
adresses_suivantes.empiler(adresse_courante)
adresse_courante = adresses_precedentes.depiler()
print(f"<- Retour vers : {adresse_courante}")
else:
print("Oh non, tu es arrivé au début de l'histoire ! Plus de pages précédentes.")
def retour_avant():
"""
Avance vers une adresse précédemment "retournée" (annule un retour).
Place la page actuelle dans adresses_precedentes avant d'avancer.
"""
global adresse_courante
global adresses_precedentes
global adresses_suivantes
if not adresses_suivantes.est_vide():
# Avant de changer l'adresse courante, on l'empile dans adresses_precedentes
# pour pouvoir revenir à cette page si on refait un "retour" classique
if adresse_courante:
adresses_precedentes.empiler(adresse_courante)
adresse_courante = adresses_suivantes.depiler()
print(f"->-> Retour avant vers : {adresse_courante}")
else:
print("Tu es déjà à la fin de ton futur proche ! Plus de pages 'retour avant'.")
# --- Tests de la simulation ---
print("Exercice 14 : Navigateur Web avec Historique 'Retour Avant'")
print("--- Début de la navigation ---")
aller_a("google.com")
aller_a("github.com")
aller_a("youtube.com")
aller_a("stack_overflow.com")
print(f"\nPage actuelle : {adresse_courante}") # stack_overflow.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # youtube.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # vide
print("\n--- On revient en arrière ---")
retour() # Retourne à youtube.com
print(f"Page actuelle : {adresse_courante}") # youtube.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # github.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # stack_overflow.com
retour() # Retourne à github.com
print(f"Page actuelle : {adresse_courante}") # github.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # google.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # youtube.com (en dessous) / stack_overflow.com (au dessus)
print("\n--- On fait un 'retour avant' ---")
retour_avant() # Avance à youtube.com
print(f"Page actuelle : {adresse_courante}") # youtube.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # github.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # stack_overflow.com
retour_avant() # Avance à stack_overflow.com
print(f"Page actuelle : {adresse_courante}") # stack_overflow.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # youtube.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # vide
print("\n--- On navigue à nouveau, cela vide l'historique 'retour avant' ---")
aller_a("new_website.com")
print(f"Page actuelle : {adresse_courante}") # new_website.com
print(f"Précédentes (sommet) : {adresses_precedentes.consulter() if not adresses_precedentes.est_vide() else 'vide'}") # stack_overflow.com
print(f"Suivantes (sommet) : {adresses_suivantes.consulter() if not adresses_suivantes.est_vide() else 'vide'}") # vide (vidé !)
print("\n--- Tentative de retour avant quand pile vide ---")
retour_avant() # Devrait dire "Plus de pages 'retour avant'."
print("-" * 20)
Explication de la correction :
L’astuce réside dans l’utilisation de deux piles :
adresses_precedentes: Pour les pages visitées avant l’actuelle. C’est l’historique « back ».adresses_suivantes: Pour les pages que tu as quittées en faisant « retour » et auxquelles tu peux « revenir en avant ». C’est l’historique « forward ».
aller_a(adresse_cible):- Si tu n’es pas sur la première page (i.e.,
adresse_couranten’est pas vide), la page actuelle est empilée dansadresses_precedentes. adresse_couranteest mise à jour avec la nouvelle cible.- Crucial :
adresses_suivantes.vider(). Si tu navigues vers une nouvelle page, tu « perds » la possibilité de faire « retour avant » aux pages que tu avais précédemment quittées par unretour(). C’est le comportement classique des navigateurs.
- Si tu n’es pas sur la première page (i.e.,
retour():- Si
adresses_precedentesn’est pas vide, tu peux revenir en arrière. - Important : L’adresse actuelle (
adresse_courante) est empilée dansadresses_suivantesavant de dépiler l’adresse précédente. C’est ce qui te permet ensuite de faire unretour_avant. adresse_couranteest mise à jour avec la page dépilée deadresses_precedentes.
- Si
retour_avant():- Si
adresses_suivantesn’est pas vide, tu peux avancer dans l’historique. - Important : L’adresse actuelle (
adresse_courante) est empilée dansadresses_precedentesavant de dépiler l’adresse deadresses_suivantes. Si tu « reviens avant », tu dois pouvoir faire « retour » sur cette page si tu changes d’avis ! adresse_couranteest mise à jour avec la page dépilée deadresses_suivantes.
- Si
C’est un bel exemple de l’utilité des piles pour gérer des historiques dynamiques ! On se croirait presque sur Internet Explorer 6… ah non, pardon, c’est moderne maintenant !
Exercice 15 : Pile Optimisée avec Attribut _taille
Énoncé
Pour éviter le problème du calcul de taille à l’exercice 13 (où taille() parcourait toute la pile), on te propose de revisiter la classe Pile en lui ajoutant un attribut privé _taille (ou simplement taille si tu préfères, mais _taille est une convention Python pour un attribut interne) indiquant à tout moment la taille de la pile.
Quelles méthodes de la classe Pile doivent être modifiées, et comment ?
Prérequis
- Avoir fait l’Exercice 13.
- Comprendre les attributs d’instance dans les classes Python.
- Savoir que l’ordre de grandeur est
O(1)pour un accès direct.
Proposition de correction
Python
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
"""structure de pile avec taille optimisée"""
def __init__(self):
self.contenu = None
self._taille = 0 # NOUVEL ATTRIBUT : on initialise la taille à 0
def est_vide(self):
return self.contenu is None
# Ou alternativement : return self._taille == 0
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
self._taille += 1 # MODIFICATION : on incrémente la taille à chaque empilement
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
self._taille -= 1 # MODIFICATION : on décrémente la taille à chaque dépilement
return v
# Méthodes additionnelles de l'exercice 13
def consulter(self):
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur
def vider(self):
self.contenu = None
self._taille = 0 # MODIFICATION : la taille redevient 0 quand on vide
def taille(self):
"""
Renvoie le nombre d'éléments dans la pile (maintenant en O(1)).
"""
return self._taille # MODIFICATION : On renvoie directement l'attribut, c'est instantané !
def creer_pile():
return Pile()
# --- Tests ---
print("Exercice 15 : Pile Optimisée avec Attribut _taille")
ma_pile_opti = creer_pile()
print(f"Taille initiale : {ma_pile_opti.taille()}") # Attend 0
ma_pile_opti.empiler("pomme")
ma_pile_opti.empiler("banane")
print(f"Taille après 2 empilements : {ma_pile_opti.taille()}") # Attend 2
ma_pile_opti.depiler()
print(f"Taille après 1 dépilement : {ma_pile_opti.taille()}") # Attend 1
ma_pile_opti.vider()
print(f"Taille après vider : {ma_pile_opti.taille()}") # Attend 0
ma_pile_opti.empiler("cerise")
print(f"Taille après nouvel empilement : {ma_pile_opti.taille()}") # Attend 1
print("-" * 20)
Quelles méthodes doivent être modifiées et comment ?
Les méthodes suivantes doivent être modifiées :
__init__(self):- Comment ? Il faut initialiser le nouvel attribut
self._taille = 0pour qu’il reflète une pile vide dès la création.
- Comment ? Il faut initialiser le nouvel attribut
empiler(self, v):- Comment ? Après avoir ajouté un élément, il faut incrémenter
self._taillede 1 (self._taille += 1).
- Comment ? Après avoir ajouté un élément, il faut incrémenter
depiler(self):- Comment ? Après avoir retiré un élément (et vérifié que la pile n’est pas vide), il faut décrémenter
self._taillede 1 (self._taille -= 1).
- Comment ? Après avoir retiré un élément (et vérifié que la pile n’est pas vide), il faut décrémenter
vider(self):- Comment ? Après avoir mis
self.contenuàNone, il faut réinitialiserself._tailleà0.
- Comment ? Après avoir mis
taille(self):- Comment ? Au lieu de parcourir la liste chaînée, cette méthode retourne simplement la valeur de
self._taille.
- Comment ? Au lieu de parcourir la liste chaînée, cette méthode retourne simplement la valeur de
Ordre de grandeur du nombre d’opérations effectuées par la fonction taille (maintenant optimisée) :
Avec l’attribut _taille, la fonction taille() ne fait plus qu’un simple accès à un attribut. C’est une opération à temps constant. L’ordre de grandeur est donc mathcalO(1). C’est le Graal de l’efficacité ! Peu importe la taille de la pile, obtenir sa taille est instantané. La contrepartie est une légère augmentation du coût des opérations empiler et depiler (une addition/soustraction en plus).
Exercice 16 : Calculatrice Polonaise Inverse (RPN)
Énoncé
L’écriture polonaise inverse (RPN) des expressions arithmétiques place l’opérateur après ses opérandes. Cette notation ne nécessite aucune parenthèse ni aucune règle de priorité. Par exemple, l’expression RPN '1 2 3 * + 4 *' désigne l’expression traditionnellement notée (1 + 2 × 3) × 4.
La valeur d’une telle expression peut être calculée facilement en utilisant une pile pour stocker les résultats intermédiaires. Pour cela, on observe un à un les éléments de l’expression et on effectue les actions suivantes :
- Si on voit un nombre, on le place sur la pile.
- Si on voit un opérateur binaire (
+ou*), on récupère les deux nombres au sommet de la pile, on leur applique l’opérateur, et on replace le résultat sur la pile.
Si l’expression était bien écrite, il y a toujours deux nombres sur la pile lorsque l’on voit un opérateur, et à la fin du processus, il reste exactement un nombre sur la pile, qui est le résultat.
Écris une fonction calculer_rpn(expression_rpn_str) prenant en paramètre une chaîne de caractères représentant une expression en notation polonaise inverse (composée d’additions et de multiplications de nombres entiers) et renvoyant la valeur de cette expression.
On supposera que les éléments de l’expression sont séparés par des espaces. Attention : Cette fonction ne doit pas renvoyer de résultat si l’expression est mal écrite. Si une condition de « mal écriture » est détectée (par exemple, pas assez d’opérandes pour un opérateur, ou trop de nombres à la fin), la fonction pourra lever une ValueError.
Prérequis
- Maîtriser la classe
Pileet ses opérations (empiler,depiler,est_vide). - Savoir manipuler les chaînes de caractères (séparer par des espaces).
- Savoir convertir des chaînes en nombres entiers (
int()). - Gérer les erreurs potentielles (
try-except).
Proposition de correction
Python
# Réutilisation de la classe Pile (avec optimisation de taille, mais pas obligatoire ici)
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
def __init__(self):
self.contenu = None
self._taille = 0 # Pour cet exercice, la taille est utile pour les vérifs
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
self._taille += 1
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
self._taille -= 1
return v
def taille(self): # On a besoin de la taille pour les vérifs d'erreur
return self._taille
def creer_pile():
return Pile()
# --- Fonction à écrire pour l'exercice ---
def calculer_rpn(expression_rpn_str):
"""
Calcule la valeur d'une expression en notation polonaise inverse (RPN).
Gère les opérateurs '+' et '*'.
Args:
expression_rpn_str (str): La chaîne de caractères représentant l'expression RPN.
Returns:
int: La valeur calculée de l'expression.
Raises:
ValueError: Si l'expression est mal formée (pas assez d'opérandes, etc.).
"""
pile_calcul = creer_pile()
elements = expression_rpn_str.split() # Sépare la chaîne en une liste d'éléments (nombres ou opérateurs)
for element in elements:
try:
# Tente de convertir l'élément en entier (c'est un nombre)
nombre = int(element)
pile_calcul.empiler(nombre)
except ValueError:
# Si ce n'est pas un nombre, c'est un opérateur
if element == '+':
if pile_calcul.taille() < 2:
raise ValueError("Erreur RPN : pas assez d'opérandes pour l'addition.")
op2 = pile_calcul.depiler() # Le premier dépilé est le deuxième opérande
op1 = pile_calcul.depiler() # Le deuxième dépilé est le premier opérande
resultat = op1 + op2
pile_calcul.empiler(resultat)
elif element == '*':
if pile_calcul.taille() < 2:
raise ValueError("Erreur RPN : pas assez d'opérandes pour la multiplication.")
op2 = pile_calcul.depiler()
op1 = pile_calcul.depiler()
resultat = op1 * op2
pile_calcul.empiler(resultat)
else:
raise ValueError(f"Erreur RPN : Opérateur inconnu '{element}'.")
# À la fin, la pile doit contenir exactement un élément : le résultat
if pile_calcul.taille() != 1:
raise ValueError("Erreur RPN : Expression mal formée ou incomplète (reste trop ou pas assez d'éléments).")
return pile_calcul.depiler() # Le résultat est le seul élément restant
# --- Tests ---
print("Exercice 16 : Calculatrice Polonaise Inverse (RPN)")
# Test 1 : L'exemple de l'énoncé
expression1 = '1 2 3 * + 4 *' # (1 + 2 * 3) * 4 = (1 + 6) * 4 = 7 * 4 = 28
print(f"Expression : '{expression1}' -> Résultat : {calculer_rpn(expression1)}") # Attend 28
# Test 2 : Une expression plus simple
expression2 = '5 2 +' # 5 + 2 = 7
print(f"Expression : '{expression2}' -> Résultat : {calculer_rpn(expression2)}") # Attend 7
# Test 3 : Une autre multiplication
expression3 = '10 3 *' # 10 * 3 = 30
print(f"Expression : '{expression3}' -> Résultat : {calculer_rpn(expression3)}") # Attend 30
# Test 4 : Une expression avec plusieurs opérations
expression4 = '7 2 + 3 *' # (7 + 2) * 3 = 9 * 3 = 27
print(f"Expression : '{expression4}' -> Résultat : {calculer_rpn(expression4)}") # Attend 27
# Test 5 : Expression mal formée (pas assez d'opérandes)
expression_mal_formee1 = '5 +'
try:
print(f"Expression : '{expression_mal_formee1}' -> Résultat : {calculer_rpn(expression_mal_formee1)}")
except ValueError as e:
print(f"Erreur attendue : {e}")
# Test 6 : Expression mal formée (trop d'opérandes à la fin)
expression_mal_formee2 = '1 2 3 +'
try:
print(f"Expression : '{expression_mal_formee2}' -> Résultat : {calculer_rpn(expression_mal_formee2)}")
except ValueError as e:
print(f"Erreur attendue : {e}")
# Test 7 : Opérateur inconnu
expression_mal_formee3 = '1 2 %'
try:
print(f"Expression : '{expression_mal_formee3}' -> Résultat : {calculer_rpn(expression_mal_formee3)}")
except ValueError as e:
print(f"Erreur attendue : {e}")
# Test 8 : Expression vide
expression_vide = ''
try:
print(f"Expression : '{expression_vide}' -> Résultat : {calculer_rpn(expression_vide)}")
except ValueError as e:
print(f"Erreur attendue : {e}") # Attend Erreur RPN : Expression mal formée ou incomplète (reste trop ou pas assez d'éléments).
print("-" * 20)
Explication de la correction :
Cet exercice est une application directe et très classique des piles !
- Initialisation : On crée une
pile_calculvide. - Découpage de l’expression : On utilise
expression_rpn_str.split()pour transformer la chaîne en une liste d’éléments (des chaînes comme'1','*','+'). - Boucle de traitement : On parcourt chaque
elementde la liste :- Si c’est un nombre : On utilise
try-except int(element)pour tenter de le convertir en entier. Si ça marche, c’est un nombre, et on l’empile. - Si c’est un opérateur : Si la conversion en entier échoue, on suppose que c’est un opérateur.
- On vérifie qu’il y a au moins deux éléments sur la pile (
pile_calcul.taille() < 2). Sinon, c’est une expression mal formée (pas assez d’opérandes), et on lève uneValueError. - On
depileles deux opérandes. Attention à l’ordre : le premier élément dépilé est le deuxième opérande (car il a été empilé en dernier), et le deuxième dépilé est le premier opérande. - On effectue l’opération (
+ou*). - Le
resultatestempileà nouveau sur la pile. - Si l’élément n’est ni un nombre ni un opérateur connu, on lève une
ValueError.
- On vérifie qu’il y a au moins deux éléments sur la pile (
- Si c’est un nombre : On utilise
- Vérification finale : Après avoir traité tous les éléments de l’expression :
- La pile doit contenir exactement un élément (
pile_calcul.taille() != 1). Si ce n’est pas le cas, l’expression est mal formée (trop de nombres, ou un opérateur manquant, etc.), et on lève uneValueError. - Le résultat final est cet unique élément restant, que l’on
depileet renvoie.
- La pile doit contenir exactement un élément (
C’est comme une petite chaîne de montage numérique, où les nombres entrent, attendent leur tour sur la pile, puis sont attrapés par des opérateurs pour créer de nouveaux nombres qui retournent en bout de file… euh, de pile !
Exercice 17 : Parenthèse Associée (Trouver l’Ouvrante)
Énoncé
On dit qu’une chaîne de caractères comprenant, entre autres choses, des parenthèses ( et ) est bien parenthésée lorsque chaque parenthèse ouvrante est associée à une unique parenthèse fermante, et réciproquement.
Écris une fonction trouver_parenthèse_ouvrante_associée(chaine, indice_fermante) prenant en paramètres une chaîne chaine (supposée bien parenthésée) et l’indice indice_fermante d’une parenthèse fermante, et qui renvoie l’indice de la parenthèse ouvrante associée.
Indice : Comme chaque parenthèse fermante est associée à la dernière parenthèse ouvrante non encore fermée, on peut suivre les associations à l’aide d’une pile. Tu y mettras les indices des parenthèses ouvrantes rencontrées.
Prérequis
- Maîtriser la classe
Pile(empiler,depiler). - Savoir parcourir une chaîne de caractères et accéder aux caractères par leur indice.
Proposition de correction
Python
# Réutilisation de la classe Pile
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def consulter(self):
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur
def creer_pile():
return Pile()
# --- Fonction à écrire pour l'exercice ---
def trouver_parenthèse_ouvrante_associée(chaine, indice_fermante):
"""
Trouve l'indice de la parenthèse ouvrante associée à une parenthèse fermante.
La chaîne est supposée bien parenthésée.
Args:
chaine (str): La chaîne de caractères.
indice_fermante (int): L'indice de la parenthèse fermante ')'.
Returns:
int: L'indice de la parenthèse ouvrante '('.
Raises:
ValueError: Si indice_fermante ne pointe pas sur une parenthèse fermante
ou si la chaîne n'est pas bien parenthésée (cas non géré par l'énoncé,
mais bonne pratique de sécurité).
"""
if chaine[indice_fermante] != ')':
raise ValueError("L'indice donné ne pointe pas sur une parenthèse fermante.")
pile_indices_ouvrantes = creer_pile()
# On parcourt la chaîne depuis le début jusqu'à l'indice de la parenthèse fermante
for i in range(indice_fermante):
caractere = chaine[i]
if caractere == '(':
pile_indices_ouvrantes.empiler(i) # On empile l'indice de chaque parenthèse ouvrante
elif caractere == ')':
# Si on rencontre une parenthèse fermante, elle ferme la dernière ouvrante non fermée.
# Donc, on dépile l'indice de cette ouvrante, car elle est maintenant "fermée".
if pile_indices_ouvrantes.est_vide():
raise ValueError("Chaîne mal parenthésée : parenthèse fermante sans ouvrante correspondante.")
pile_indices_ouvrantes.depiler()
# Quand on arrive à l'indice_fermante, le sommet de la pile doit être l'indice de son ouvrante associée
if pile_indices_ouvrantes.est_vide():
raise ValueError("Chaîne mal parenthésée : parenthèse fermante sans ouvrante correspondante (problème d'indice).")
return pile_indices_ouvrantes.depiler() # Le sommet est l'indice recherché !
# --- Tests ---
print("Exercice 17 : Parenthèse Associée (Trouver l'Ouvrante)")
chaine1 = "((A+B)*(C-D))"
# Indices : 0123456789012
# Caractères : ((A+B)*(C-D))
# indice_fermante : 6 (pour le premier ')'), 12 (pour le dernier ')')
print(f"Chaîne : '{chaine1}'")
print(f"Indice fermante 6 (')') : ouvrante à l'indice {trouver_parenthèse_ouvrante_associée(chaine1, 6)}") # Attend 2
print(f"Indice fermante 12 (')') : ouvrante à l'indice {trouver_parenthèse_ouvrante_associée(chaine1, 12)}") # Attend 0
chaine2 = "(X(Y)Z)"
# Indices : 0123456
# Caractères : (X(Y)Z)
print(f"\nChaîne : '{chaine2}'")
print(f"Indice fermante 4 (')') : ouvrante à l'indice {trouver_parenthèse_ouvrante_associée(chaine2, 4)}") # Attend 2
print(f"Indice fermante 6 (')') : ouvrante à l'indice {trouver_parenthèse_ouvrante_associée(chaine2, 6)}") # Attend 0
# Test avec une chaîne simple
chaine3 = "(coucou)"
print(f"\nChaîne : '{chaine3}'")
print(f"Indice fermante 7 (')') : ouvrante à l'indice {trouver_parenthèse_ouvrante_associée(chaine3, 7)}") # Attend 0
# Test d'erreur (si l'énoncé n'avait pas supposé "bien parenthésée")
try:
chaine_mal_formee = "())("
trouver_parenthèse_ouvrante_associée(chaine_mal_formee, 2)
except ValueError as e:
print(f"\nErreur attendue : {e}") # Chaîne mal parenthésée : parenthèse fermante sans ouvrante correspondante.
print("-" * 20)
Explication de la correction :
Ce problème est un autre exemple classique de l’utilisation des piles pour la gestion des structures imbriquées (comme les parenthèses, les balises HTML/XML, etc.).
- Initialisation : On crée une pile
pile_indices_ouvrantes. Cette pile stockera les indices des parenthèses ouvrantes(que l’on rencontre. - Parcours de la chaîne : On parcourt la chaîne caractère par caractère, de l’indice
0jusqu’àindice_fermante - 1(on ne traite pas encore la parenthèse fermante cible).- Si
caractere == '(': On a trouvé une parenthèse ouvrante. Onempilesonindicedans la pile. - Si
caractere == ')': On a trouvé une parenthèse fermante. Elle ferme la dernière parenthèse ouvrante qui a étéempileeet qui n’a pas encore été fermée. Ondepiledonc l’indice du sommet de la pile. Cela signifie que cette paire est maintenant « résolue ».
- Si
- Arrivée à
indice_fermante: Quand la boucle se termine (c’est-à-dire quandiatteintindice_fermante), la parenthèse fermante àindice_fermantedoit obligatoirement correspondre à la parenthèse ouvrante qui est au sommet de la pile (la dernière non fermée). Ondepilecet indice et on le renvoie.
Si la chaîne est « bien parenthésée » comme le suppose l’énoncé, la pile ne devrait jamais être vide quand on essaie de depiler une parenthèse ouvrante, et il devrait rester exactement un élément au sommet de la pile quand on atteint l’indice_fermante. J’ai ajouté quelques ValueError pour gérer les cas (même si non attendus par l’énoncé) où la chaîne ne serait pas bien parenthésée.
C’est comme un jeu de cache-cache : chaque ( se cache dans la pile, et quand un ) apparaît, il attrape le dernier ( caché !
Exercice 18 : Vérification de Chaînes Bien Parenthésées (Multiples Types)
Énoncé
On considère une chaîne de caractères incluant à la fois des parenthèses rondes ( et ) et des parenthèses carrées [ et ]. La chaîne est bien parenthésée si chaque ouvrante est associée à une unique fermante de même forme, et réciproquement.
Écris une fonction est_bien_parenthésée(chaine) prenant en paramètre une chaîne de caractères (contenant, entre autres, les parenthèses décrites) et qui renvoie True si la chaîne est bien parenthésée et False sinon.
Prérequis
- Avoir compris l’Exercice 17.
- Savoir utiliser une pile pour faire correspondre des ouvrantes/fermantes.
- Gérer plusieurs types de parenthèses et s’assurer qu’elles correspondent correctement (forme et ordre).
Proposition de correction
Python
# Réutilisation de la classe Pile
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def consulter(self):
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.contenu.valeur
def taille(self): # Utile pour la vérif finale
compteur = 0
courant = self.contenu
while courant is not None:
compteur += 1
courant = courant.suivante
return compteur
def creer_pile():
return Pile()
# --- Fonction à écrire pour l'exercice ---
def est_bien_parenthésée(chaine):
"""
Vérifie si une chaîne de caractères est bien parenthésée avec '(' ')' et '[' ']'.
Args:
chaine (str): La chaîne à vérifier.
Returns:
bool: True si la chaîne est bien parenthésée, False sinon.
"""
pile_parenthèses_ouvrantes = creer_pile()
# Dictionnaire pour associer chaque parenthèse fermante à son ouvrante correspondante
paires_parenthèses = {')': '(', ']': '['}
for caractere in chaine:
if caractere in ['(', '[']:
# Si c'est une parenthèse ouvrante, on l'empile
pile_parenthèses_ouvrantes.empiler(caractere)
elif caractere in [')', ']']:
# Si c'est une parenthèse fermante
if pile_parenthèses_ouvrantes.est_vide():
return False # Il y a une parenthèse fermante sans parenthèse ouvrante correspondante
# On dépile la dernière parenthèse ouvrante
derniere_ouvrante = pile_parenthèses_ouvrantes.depiler()
# On vérifie si la parenthèse ouvrante dépilée correspond à la fermante actuelle
if paires_parenthèses[caractere] != derniere_ouvrante:
return False # La forme ne correspond pas (ex: (] )
# À la fin, la pile doit être vide. Si elle ne l'est pas,
# il reste des parenthèses ouvrantes non fermées.
return pile_parenthèses_ouvrantes.est_vide()
# --- Tests ---
print("Exercice 18 : Vérification de Chaînes Bien Parenthésées (Multiples Types)")
print(f"'([])' est bien parenthésée : {est_bien_parenthésée('([])')}") # Attend True
print(f"'([{}])' est bien parenthésée : {est_bien_parenthésée('([{}]')}") # FAUX : l'énoncé n'incluait pas {}, donc False attendu
# Pour le test, je vais m'en tenir à '(' ')' '[' ']'
print(f"'([()])' est bien parenthésée : {est_bien_parenthésée('([()])')}") # Attend True
print(f"'(' est bien parenthésée : {est_bien_parenthésée('(')}") # Attend False (non fermée)
print(f"')' est bien parenthésée : {est_bien_parenthésée(')')}") # Attend False (fermante sans ouvrante)
print(f"'([)]' est bien parenthésée : {est_bien_parenthésée('([)]')}") # Attend False (mismatch de type)
print(f"'[)' est bien parenthésée : {est_bien_parenthésée('[)')}") # Attend False (mismatch de type)
print(f"'' (vide) est bien parenthésée : {est_bien_parenthésée('')}") # Attend True
print(f"'(a[b]c)' est bien parenthésée : {est_bien_parenthésée('(a[b]c)')}") # Attend True (autres caractères ignorés)
print(f"'](' est bien parenthésée : {est_bien_parenthésée('](')}") # Attend False (fermante sans ouvrante)
print("-" * 20)
Explication de la correction :
Cet exercice est une extension de l’Exercice 17. Le principe est le même, mais il faut gérer plusieurs types de parenthèses.
- Initialisation : On crée une pile
pile_parenthèses_ouvrantespour stocker les parenthèses ouvrantes que l’on rencontre. On ajoute un dictionnairepaires_parenthèsesqui associe chaque parenthèse fermante à sa parenthèse ouvrante correspondante. - Parcours de la chaîne : On parcourt la chaîne caractère par caractère :
- Si
caractereest une parenthèse ouvrante ((ou[) : On l’empile. - Si
caractereest une parenthèse fermante ()ou]) :- On vérifie si la pile est vide. Si oui, cela signifie qu’on a trouvé une parenthèse fermante sans ouvrante correspondante, donc la chaîne est mal parenthésée (
return False). - Si la pile n’est pas vide, on
depilel’élément au sommet. C’est la dernière parenthèse ouvrante non fermée. - On compare cette
derniere_ouvranteavec la parenthèse ouvrante attendue pour lacaracterefermante actuelle (viapaires_parenthèses[caractere]). Si elles ne correspondent pas (ex: on attend(mais on dépile[), la chaîne est mal parenthésée (return False).
- On vérifie si la pile est vide. Si oui, cela signifie qu’on a trouvé une parenthèse fermante sans ouvrante correspondante, donc la chaîne est mal parenthésée (
- Autres caractères : Si le caractère n’est pas une parenthèse, on l’ignore (il ne perturbe pas l’appariement des parenthèses).
- Si
- Vérification finale : Après avoir parcouru toute la chaîne :
- Si la pile est vide, cela signifie que toutes les parenthèses ouvrantes ont trouvé leur correspondante fermante. La chaîne est bien parenthésée (
return True). - Si la pile n’est pas vide, cela signifie qu’il reste des parenthèses ouvrantes qui n’ont jamais été fermées. La chaîne est mal parenthésée (
return False).
- Si la pile est vide, cela signifie que toutes les parenthèses ouvrantes ont trouvé leur correspondante fermante. La chaîne est bien parenthésée (
Cette fonction est comme un arbitre de boxe pour parenthèses : il s’assure que chaque parenthèse ouvrante trouve son match du même type, et que personne ne reste sur le carreau à la fin !
Exercice 19 : Calculatrice Ordinaire (Priorités et Parenthèses)
Énoncé
On souhaite réaliser un programme évaluant une expression arithmétique donnée par une chaîne de caractères. On utilisera les notations et les règles de priorité ordinaires, en supposant pour simplifier que chaque élément est séparé des autres par une espace. Exemple : '( 1 + 2 * 3 ) * 4'.
Comme dans l’exercice 16, nous allons parcourir l’expression de gauche à droite et utiliser une pile. On alterne entre deux opérations : ajouter un nouvel élément sur la pile, et simplifier une opération présente au sommet de la pile.
Pour réaliser cela, on suit un algorithme qui, pour chaque élément de l’expression en entrée, applique les critères suivants :
- Si l’élément est un nombre, on place sa valeur sur la pile.
- Si l’élément est une parenthèse
(, on la place sur la pile. - Si l’élément est une parenthèse
), on simplifie toutes les opérations possibles au sommet de la pile. À la fin, le sommet de la pile doit contenir un entiernprécédé d’une parenthèse ouvrante(, parenthèse que l’on retire pour ne garder quen. - Si l’élément est un opérateur (
+,*, …), on simplifie toutes les opérations au sommet de la pile utilisant des opérateurs aussi prioritaires ou plus prioritaires que le nouvel opérateur, puis on place ce dernier sur la pile.
Écris une fonction simplifier_operations(pile, operateurs_prioritaires) qui simplifie toutes les opérations au sommet de pile utilisant un opérateur de l’ensemble operateurs_prioritaires. Ensuite, déduis-en une fonction calculer_expression(expression_str) renvoyant la valeur de l’expression.
Note : Cet exercice fait une « entorse » à la bonne pratique de ne toujours utiliser les piles que de manière homogène, puisque notre pile contiendra à la fois des symboles (chaînes de caractères) et des nombres entiers. C’est un cas d’usage courant pour ce type de problème.
Prérequis
- Avoir fait l’Exercice 16 (Calculatrice RPN) pour la base des opérations.
- Maîtriser les piles.
- Comprendre les règles de priorité des opérateurs et la gestion des parenthèses.
- Ce sera une fonction plus complexe, prenant en compte le type de l’élément au sommet de la pile.
Proposition de correction
Python
# Réutilisation de la classe Pile (pour des éléments hétérogènes)
class Cellule:
def __init__(self, v, s):
self.valeur = v
self.suivante = s
class Pile:
def __init__(self):
self.contenu = None
def est_vide(self):
return self.contenu is None
def empiler(self, v):
self.contenu = Cellule(v, self.contenu)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
v = self.contenu.valeur
self.contenu = self.contenu.suivante
return v
def consulter(self):
if self.est_vide():
return None # Retourne None au lieu de lever une erreur pour faciliter les vérifs
return self.contenu.valeur
def taille(self):
compteur = 0
courant = self.contenu
while courant is not None:
compteur += 1
courant = courant.suivante
return compteur
def creer_pile():
return Pile()
# --- Fonctions à écrire pour l'exercice ---
# Dictionnaire des priorités des opérateurs (plus le nombre est grand, plus la priorité est élevée)
PRIORITES_OPERATEURS = {
'+': 1,
'*': 2
}
def appliquer_operateur(op, op1, op2):
"""Applique l'opérateur sur les deux opérandes."""
if op == '+':
return op1 + op2
elif op == '*':
return op1 * op2
else:
raise ValueError(f"Opérateur inconnu : {op}")
def simplifier_operations(pile, operateurs_prioritaires):
"""
Simplifie les opérations au sommet de la pile si l'opérateur est dans operateurs_prioritaires.
Continue tant qu'il y a un opérateur pertinent au sommet.
Args:
pile (Pile): La pile contenant les éléments de l'expression.
operateurs_prioritaires (set): Un ensemble d'opérateurs à simplifier.
Raises:
ValueError: Si la pile est mal formée pour l'opération.
"""
while True:
# On vérifie qu'il y a au moins 3 éléments pour une opération (op1, op, op2)
if pile.taille() < 3:
break # Pas assez d'éléments pour une opération
# Le sommet de la pile doit être un nombre (op2)
op2_val = pile.consulter()
if not isinstance(op2_val, (int, float)): # On accepte int/float pour les nombres
break # Le sommet n'est pas un nombre, on ne peut pas simplifier une opération
pile.depiler() # Dépile op2
# Le nouvel sommet doit être un opérateur
operateur = pile.consulter()
if not isinstance(operateur, str) or operateur not in operateurs_prioritaires:
pile.empiler(op2_val) # On remet op2 car l'opérateur ne nous intéresse pas
break # Pas l'opérateur désiré au sommet, ou ce n'est pas une chaîne
pile.depiler() # Dépile l'opérateur
# L'avant-dernier élément doit être un nombre (op1)
op1_val = pile.consulter()
if not isinstance(op1_val, (int, float)):
# Oh non, la pile est mal formée ! On remet tout et on lève l'erreur.
pile.empiler(operateur)
pile.empiler(op2_val)
raise ValueError("Pile mal formée : opérande manquant avant un opérateur.")
pile.depiler() # Dépile op1
# On applique l'opération et on empile le résultat
resultat = appliquer_operateur(operateur, op1_val, op2_val)
pile.empiler(resultat)
def calculer_expression(expression_str):
"""
Évalue une expression arithmétique avec priorités et parenthèses.
Args:
expression_str (str): La chaîne de caractères de l'expression.
Returns:
int or float: La valeur de l'expression.
Raises:
ValueError: Si l'expression est mal formée.
"""
pile = creer_pile()
elements = expression_str.split()
for element in elements:
try:
# Si c'est un nombre, l'empiler
nombre = int(element)
pile.empiler(nombre)
except ValueError:
# Si ce n'est pas un nombre, c'est un symbole
if element == '(':
pile.empiler(element)
elif element == ')':
# Simplifier toutes les opérations jusqu'à la parenthèse ouvrante
simplifier_operations(pile, set(PRIORITES_OPERATEURS.keys())) # Simplifie tous les opérateurs
# Vérifier que le sommet est un nombre et l'avant-dernier une '('
if pile.est_vide() or not isinstance(pile.consulter(), (int, float)):
raise ValueError("Parenthèse fermante inattendue ou expression mal formée (pas de nombre avant ')').")
resultat_parenthèse = pile.depiler() # Le résultat de l'opération entre parenthèses
if pile.est_vide() or pile.depiler() != '(': # L'avant-dernier doit être '(' et on le retire
raise ValueError("Parenthèse fermante sans parenthèse ouvrante correspondante.")
pile.empiler(resultat_parenthèse) # Empiler le résultat de la parenthèse
elif element in PRIORITES_OPERATEURS:
# Si c'est un opérateur, simplifier les opérateurs de priorité égale ou supérieure
operateurs_a_simplifier = {op for op, prio in PRIORITES_OPERATEURS.items()
if prio >= PRIORITES_OPERATEURS[element]}
simplifier_operations(pile, operateurs_a_simplifier)
pile.empiler(element) # Empiler le nouvel opérateur
else:
raise ValueError(f"Élément inconnu dans l'expression : '{element}'.")
# Après avoir parcouru tous les éléments, simplifier toutes les opérations restantes
simplifier_operations(pile, set(PRIORITES_OPERATEURS.keys()))
# À la fin, la pile doit contenir un seul élément : le résultat final
if pile.taille() != 1 or not isinstance(pile.consulter(), (int, float)):
raise ValueError("Expression mal formée ou incomplète (reste trop ou pas assez d'éléments, ou pas un nombre final).")
return pile.depiler()
# --- Tests ---
print("Exercice 19 : Calculatrice Ordinaire")
# Exemple de l'énoncé : (1 + 2 * 3) * 4 = (1 + 6) * 4 = 7 * 4 = 28
expr1 = '( 1 + 2 * 3 ) * 4'
print(f"'{expr1}' = {calculer_expression(expr1)}") # Attend 28
# Exemple simple
expr2 = '5 + 2 * 3' # 5 + 6 = 11
print(f"'{expr2}' = {calculer_expression(expr2)}") # Attend 11
# Autre exemple
expr3 = '( 10 - 5 ) * 2' # N'inclut pas le '-' par défaut, donc erreur attendue
try:
print(f"'{expr3}' = {calculer_expression(expr3)}")
except ValueError as e:
print(f"Erreur attendue : {e}") # Élément inconnu : '-'
# Pour que ça marche avec -, il faut l'ajouter :
PRIORITES_OPERATEURS['-'] = 1 # Même priorité que +
def appliquer_operateur_full(op, op1, op2):
if op == '+': return op1 + op2
elif op == '*': return op1 * op2
elif op == '-': return op1 - op2
else: raise ValueError(f"Opérateur inconnu : {op}")
# Et modifier la fonction simplifier_operations pour utiliser cette nouvelle fonction
# Pour rester fidèle à l'exercice original, je n'implémente pas ça ici.
expr4 = '2 * ( 3 + 4 )' # 2 * 7 = 14
print(f"'{expr4}' = {calculer_expression(expr4)}") # Attend 14
expr5 = '1 + 2 + 3 + 4' # 10
print(f"'{expr5}' = {calculer_expression(expr5)}") # Attend 10
expr6 = '( ( 1 + 2 ) * 3 )' # (3 * 3) = 9
print(f"'{expr6}' = {calculer_expression(expr6)}") # Attend 9
# Tests d'erreur
expr_err1 = '1 + * 2'
try:
print(f"'{expr_err1}' = {calculer_expression(expr_err1)}")
except ValueError as e:
print(f"Erreur attendue : {e}") # Pile mal formée : opérande manquant...
expr_err2 = '( 1 + 2'
try:
print(f"'{expr_err2}' = {calculer_expression(expr_err2)}")
except ValueError as e:
print(f"Erreur attendue : {e}") # Expression mal formée ou incomplète...
expr_err3 = '1 + )'
try:
print(f"'{expr_err3}' = {calculer_expression(expr_err3)}")
except ValueError as e:
print(f"Erreur attendue : {e}") # Parenthèse fermante sans parenthèse ouvrante correspondante.
print("-" * 20)
Explication de la correction :
Cet exercice est le boss final de la manipulation de piles pour les expressions arithmétiques ! Il implémente l’algorithme de Shunting-yard simplifié (ou un équivalent) pour évaluer les expressions.
PRIORITES_OPERATEURS: Un dictionnaire pour stocker la priorité de chaque opérateur. Plus le nombre est grand, plus l’opérateur est prioritaire.appliquer_operateur(op, op1, op2): Une fonction utilitaire pour effectuer l’opération.simplifier_operations(pile, operateurs_prioritaires): C’est le cœur de la logique de simplification :- Elle boucle tant qu’il y a potentiellement une opération à simplifier.
- Elle vérifie qu’il y a suffisamment d’éléments pour une opération (opérande2, opérateur, opérande1).
- Elle
depilel’opérande2, puis l’opérateur. - Crucial : Elle vérifie si l’opérateur dépilé fait partie des
operateurs_prioritaires(ceux que l’on veut simplifier à ce moment précis). Si non, elle rempile l’opérateur et l’opérande2 et s’arrête (car cet opérateur n’est pas à simplifier maintenant). - Si l’opérateur est pertinent, elle
depilel’opérande1. - Elle applique l’opération et
empilele résultat.
calculer_expression(expression_str): La fonction principale :- Elle parcourt les
elementsde l’expression. - Nombre : Empile le nombre.
- Parenthèse ouvrante
(: Empile simplement le caractère(. - Parenthèse fermante
):- Appelle
simplifier_operationsavec tous les opérateurs possibles (PRIORITES_OPERATEURS.keys()). Cela va résoudre tout ce qui se trouve à l’intérieur des parenthèses. - Après la simplification, le sommet de la pile doit être le résultat de l’expression entre parenthèses, et juste en dessous, il doit y avoir la parenthèse ouvrante
(. Ondepilele résultat, puis ondepileet vérifie le(. Enfin, onempilele résultat de la parenthèse.
- Appelle
- Opérateur (
+ou*) :- Détermine les opérateurs
operateurs_a_simplifierqui ont une priorité égale ou supérieure à l’opérateur actuel. - Appelle
simplifier_operationsavec cet ensemble d’opérateurs pour résoudre les opérations précédentes de haute priorité. - Enfin,
empilel’opérateur actuel.
- Détermine les opérateurs
- Fin de l’expression : Après avoir traité tous les éléments, on appelle
simplifier_operationsune dernière fois avec tous les opérateurs pour vider la pile et obtenir le résultat final. - Vérification finale : La pile doit contenir un unique nombre, qui est le résultat.
- Elle parcourt les
C’est un algorithme ingénieux qui utilise la pile pour respecter les règles de priorité (ce qui est plus prioritaire est calculé plus tôt) et les parenthèses (elles forcent la simplification immédiate de ce qu’elles contiennent). Bravo si tu as réussi à le déchiffrer et à l’implémenter, c’est de la haute voltige !
Exercice 20 : Pile Bornée (Implémentation par Tableau)
Énoncé
Une pile bornée est une pile dotée à sa création d’une capacité maximale. On propose l’interface suivante :
| Fonction | Description |
creer_pile(c) | Crée et renvoie une pile bornée de capacité c. |
est_vide(p) | Renvoie True si la pile est vide et False sinon. |
est_pleine(p) | Renvoie True si la pile est pleine et False sinon. |
empiler(p, e) | Ajoute e au sommet de p si p n’est pas pleine, et lève une exception IndexError sinon. |
depiler(p) | Retire et renvoie l’élément au sommet de p si p n’est pas vide, et lève une exception IndexError sinon. |
Exporter vers Sheets
On propose de réaliser une telle pile bornée à l’aide d’un tableau (liste Python native) dont la taille est fixée à la création et correspond à la capacité. Les éléments de la pile sont stockés consécutivement à partir de l’indice 0 (qui contient l’élément du fond de la pile). On se donne également un entier enregistrant le nombre d’éléments dans la pile, qui permet donc également de désigner l’indice de la prochaine case libre. Ainsi, les éléments sont ajoutés et retirés du côté droit du tableau :
Indices : 0 1 ... nb-1 nb ... capacité-1
| | ... | | ... |
Contenu : [ a , b , ... z , None , ... None ]
^
|
(Prochaine case libre)
Réalise une telle structure à l’aide d’une classe ayant pour attributs le tableau fixe et le nombre d’éléments dans la pile bornée.
Prérequis
- Comprendre le concept de pile bornée.
- Savoir manipuler les listes Python natives (qui simulent un tableau).
- Gérer les indices dans un tableau.
- Connaître les opérations d’ajout/retrait pour une pile LIFO.
Proposition de correction
Python
class PileBornee:
"""Structure de pile bornée implémentée avec un tableau (liste Python)."""
def __init__(self, capacite):
if capacite <= 0:
raise ValueError("La capacité d'une pile bornée doit être positive.")
self.capacite = capacite
self.tableau = [None] * capacite # Le tableau fixe de taille 'capacite'
self.nb_elements = 0 # Indique le nombre d'éléments et l'indice de la prochaine case libre
def est_vide(self):
return self.nb_elements == 0
def est_pleine(self):
return self.nb_elements == self.capacite
def empiler(self, e):
if self.est_pleine():
raise IndexError("empiler sur une pile pleine")
self.tableau[self.nb_elements] = e # On ajoute l'élément à l'indice de la prochaine case libre
self.nb_elements += 1 # On incrémente le nombre d'éléments (qui devient le nouvel indice de la case libre)
def depiler(self):
if self.est_vide():
raise IndexError("depiler sur une pile vide")
self.nb_elements -= 1 # On décrémente le nombre d'éléments pour pointer sur le dernier
valeur = self.tableau[self.nb_elements] # On récupère l'élément au sommet
self.tableau[self.nb_elements] = None # Optionnel: "vider" la case (pour le ramasse-miettes)
return valeur
def consulter(self): # Utile pour les tests, comme à l'exercice 13
if self.est_vide():
raise IndexError("consulter sur une pile vide")
return self.tableau[self.nb_elements - 1] # Le sommet est le dernier élément ajouté
def creer_pile_bornee(c):
return PileBornee(c)
# --- Tests ---
print("Exercice 20 : Pile Bornée (Implémentation par Tableau)")
ma_pile_bornee = creer_pile_bornee(3) # Capacité de 3
print(f"Pile vide ? {ma_pile_bornee.est_vide()}") # Attend True
print(f"Pile pleine ? {ma_pile_bornee.est_pleine()}") # Attend False
print(f"Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 0
ma_pile_bornee.empiler("pomme")
print(f"Empilé 'pomme'. Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 1
print(f"Sommet : {ma_pile_bornee.consulter()}") # Attend 'pomme'
ma_pile_bornee.empiler("banane")
print(f"Empilé 'banane'. Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 2
print(f"Sommet : {ma_pile_bornee.consulter()}") # Attend 'banane'
ma_pile_bornee.empiler("cerise")
print(f"Empilé 'cerise'. Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 3
print(f"Sommet : {ma_pile_bornee.consulter()}") # Attend 'cerise'
print(f"Pile pleine ? {ma_pile_bornee.est_pleine()}") # Attend True
# Test d'empilement sur pile pleine
try:
ma_pile_bornee.empiler("kiwi")
except IndexError as e:
print(f"Erreur attendue : {e}")
print(f"Dépilé : {ma_pile_bornee.depiler()}") # Attend 'cerise'
print(f"Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 2
print(f"Sommet : {ma_pile_bornee.consulter()}") # Attend 'banane'
print(f"Pile pleine ? {ma_pile_bornee.est_pleine()}") # Attend False
ma_pile_bornee.depiler()
ma_pile_bornee.depiler()
print(f"Nombre d'éléments : {ma_pile_bornee.nb_elements}") # Attend 0
print(f"Pile vide ? {ma_pile_bornee.est_vide()}") # Attend True
# Test de dépilement sur pile vide
try:
ma_pile_bornee.depiler()
except IndexError as e:
print(f"Erreur attendue : {e}")
print("-" * 20)
Explication de la correction :
L’implémentation d’une pile avec un tableau est très efficace !
__init__(self, capacite):- On stocke la
capacitemaximale. - On crée un
self.tableau(une liste Python) de la taille spécifiée, remplie deNone(ou n’importe quelle valeur par défaut). self.nb_elementsest le compteur crucial : il indique non seulement le nombre d’éléments, mais aussi le premier indice disponible pour le prochainempiler, et l’indice du dernier élémentnb_elements - 1.
- On stocke la
est_vide()etest_pleine():- Elles sont directes : on compare
self.nb_elementsà 0 ou àself.capacite.
- Elles sont directes : on compare
empiler(self, e):- On vérifie d’abord si la pile n’est pas pleine. Si elle l’est, on lève une
IndexError. - On place le nouvel élément
eà l’indiceself.nb_elements(qui est la première case libre). - On incrémente
self.nb_elements.
- On vérifie d’abord si la pile n’est pas pleine. Si elle l’est, on lève une
depiler(self):- On vérifie d’abord si la pile n’est pas vide. Si elle l’est, on lève une
IndexError. - On décrémente
self.nb_elements. Maintenant,self.nb_elementspointe sur l’indice du dernier élément valide qui vient d’être dépilé. - On récupère la
valeurà cet indice. - Optionnel mais bonne pratique :
self.tableau[self.nb_elements] = Nonepour « vider » la case et aider le ramasse-miettes à libérer la mémoire si l’objet n’est plus référencé ailleurs. - On renvoie la
valeur.
- On vérifie d’abord si la pile n’est pas vide. Si elle l’est, on lève une
consulter(self):- Si la pile est vide, erreur.
- Sinon, le sommet est toujours à l’indice
self.nb_elements - 1.
Cette implémentation est super rapide ! Toutes les opérations (empiler, depiler, est_vide, est_pleine, consulter, taille) se font en temps constant, mathcalO(1), car elles ne nécessitent qu’un accès direct au tableau ou à un attribut, sans boucle. C’est comme avoir un accès direct au dernier livre posé sur la pile, sans avoir à parcourir toute la bibliothèque !
Exercice 21 : File Bornée (Implémentation par Tableau Circulaire)
Énoncé
Une file bornée est une file dotée à sa création d’une capacité maximale. On propose l’interface suivante :
| Fonction | Description |
creer_file(c) | Crée et renvoie une file bornée de capacité c. |
est_vide(f) | Renvoie True si la file est vide et False sinon. |
est_pleine(f) | Renvoie True si la file est pleine et False sinon. |
ajouter(f, e) | Ajoute e à l’arrière de f si f n’est pas pleine, et lève une exception IndexError sinon. |
retirer(f) | Retire et renvoie l’élément à l’avant de f si f n’est pas vide, et lève une exception IndexError sinon. |
Exporter vers Sheets
Comme pour la pile bornée (exercice 20), on propose de réaliser une telle file bornée à l’aide d’un tableau dont la taille est fixée à la création et correspond à la capacité. Les éléments de la file sont stockés consécutivement à partir d’un indice premier correspondant à l’avant de la file, et le tableau est considéré comme circulaire : après la dernière case, les éléments reviennent à la première.
Dans ce schéma, un élément retiré l’est au niveau de l’indice premier, et un élément ajouté l’est à l’autre extrémité.
État 1 : File non pleine
Indices : 0 ... premier ... (premier+nb-1)%cap ... capacité-1
| | |
Contenu : [None, ..., None, ..., a , b , ... z , None, ..., None]
^ ^
| |
premier (premier+nb)%cap (prochaine place pour ajouter)
État 2 : File circulaire (les éléments "débordent")
Indices : 0 ... (premier+nb-1)%cap ... premier-1 premier ... capacité-1
| | | |
Contenu : [ k , l , ... z , None, ..., None, a , b , ... j ]
^ ^ ^
| | |
(premier+nb)%cap premier (premier+nb)%cap si vide
Réalise une telle structure à l’aide d’une classe ayant pour attributs :
- le tableau fixe (
self.tableau), - le nombre d’éléments dans la file bornée (
self.nb_elements), - l’indice du premier élément (
self.premier_indice).
Prérequis
- Comprendre le concept de file bornée et le principe FIFO.
- Savoir manipuler les listes Python natives.
- Maîtriser l’arithmétique modulo (
%) pour la gestion circulaire des indices. - Gérer les cas d’insertion et de retrait à différentes extrémités.
Proposition de correction
Python
class FileBornee:
"""Structure de file bornée implémentée avec un tableau circulaire."""
def __init__(self, capacite):
if capacite <= 0:
raise ValueError("La capacité d'une file bornée doit être positive.")
self.capacite = capacite
self.tableau = [None] * capacite # Le tableau fixe
self.nb_elements = 0 # Nombre d'éléments actuellement dans la file
self.premier_indice = 0 # Indice du premier élément (tête de la file)
# L'indice de la prochaine case où ajouter un élément sera :
# (self.premier_indice + self.nb_elements) % self.capacite
def est_vide(self):
return self.nb_elements == 0
def est_pleine(self):
return self.nb_elements == self.capacite
def ajouter(self, e):
if self.est_pleine():
raise IndexError("ajouter sur une file pleine")
# Calcul de l'indice où ajouter le nouvel élément
# C'est (premier_indice + nombre_elements) % capacite
indice_ajout = (self.premier_indice + self.nb_elements) % self.capacite
self.tableau[indice_ajout] = e
self.nb_elements += 1 # Incrémente le nombre d'éléments
def retirer(self):
if self.est_vide():
raise IndexError("retirer d'une file vide")
valeur = self.tableau[self.premier_indice] # Récupère l'élément à la tête
self.tableau[self.premier_indice] = None # Optionnel: "vider" la case
# Avance l'indice du premier élément de manière circulaire
self.premier_indice = (self.premier_indice + 1) % self.capacite
self.nb_elements -= 1 # Décrémente le nombre d'éléments
return valeur
def consulter_premier(self): # Méthode ajoutée pour consulter le premier sans le retirer
if self.est_vide():
raise IndexError("consulter sur une file vide")
return self.tableau[self.premier_indice]
def creer_file_bornee(c):
return FileBornee(c)
# --- Tests ---
print("Exercice 21 : File Bornée (Implémentation par Tableau Circulaire)")
ma_file_bornee = creer_file_bornee(4) # Capacité de 4
print(f"File vide ? {ma_file_bornee.est_vide()}") # True
print(f"File pleine ? {ma_file_bornee.est_pleine()}") # False
print(f"Nombre d'éléments : {ma_file_bornee.nb_elements}") # 0
print(f"Premier indice : {ma_file_bornee.premier_indice}") # 0
print(f"Tableau initial : {ma_file_bornee.tableau}") # [None, None, None, None]
ma_file_bornee.ajouter("Client A")
print(f"\nAjout Client A. Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 1, Premier: 0, Tableau: ['Client A', None, None, None]
ma_file_bornee.ajouter("Client B")
print(f"Ajout Client B. Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 2, Premier: 0, Tableau: ['Client A', 'Client B', None, None]
print(f"\nConsultation premier : {ma_file_bornee.consulter_premier()}") # Attendu: Client A
print(f"Retrait : {ma_file_bornee.retirer()}") # Attendu: Client A
print(f"Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 1, Premier: 1, Tableau: [None, 'Client B', None, None]
ma_file_bornee.ajouter("Client C")
ma_file_bornee.ajouter("Client D")
ma_file_bornee.ajouter("Client E") # La file devrait être pleine après ça
print(f"\nAjouts C, D, E. Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 4, Premier: 1, Tableau: ['Client E', 'Client B', 'Client C', 'Client D']
# 'Client B' à indice 1, 'Client C' à indice 2, 'Client D' à indice 3, 'Client E' à indice 0 (circulaire)
print(f"File pleine ? {ma_file_bornee.est_pleine()}") # True
# Test d'ajout sur file pleine
try:
ma_file_bornee.ajouter("Client F")
except IndexError as e:
print(f"Erreur attendue : {e}")
print(f"\nRetrait : {ma_file_bornee.retirer()}") # Attendu: Client B
print(f"Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 3, Premier: 2, Tableau: [None, None, 'Client C', 'Client D']
print(f"Retrait : {ma_file_bornee.retirer()}") # Attendu: Client C
print(f"Retrait : {ma_file_bornee.retirer()}") # Attendu: Client D
print(f"Retrait : {ma_file_bornee.retirer()}") # Attendu: Client E (le dernier via l'enroulement)
print(f"Nbr éléments: {ma_file_bornee.nb_elements}, Premier indice: {ma_file_bornee.premier_indice}, Tableau: {ma_file_bornee.tableau}")
# Attendu: Nbr: 0, Premier: 1 (revient à 1 après avoir retiré E), Tableau: [None, None, None, None]
print(f"File vide ? {ma_file_bornee.est_vide()}") # True
# Test de retrait sur file vide
try:
ma_file_bornee.retirer()
except IndexError as e:
print(f"Erreur attendue : {e}")
print("-" * 20)
Explication de la correction :
L’implémentation d’une file bornée avec un tableau circulaire est un peu plus délicate que la pile, mais tout aussi efficace une fois maîtrisée. Le secret, c’est l’opérateur modulo (%) !
__init__(self, capacite):self.capacite: La taille fixe du tableau.self.tableau: Le tableau lui-même, initialisé avecNone.self.nb_elements: Le nombre actuel d’éléments dans la file.self.premier_indice: C’est l’indice dans le tableau où se trouve le premier élément de la file (la tête). Quand la file est vide, cet indice peut être n’importe quoi, mais 0 est une bonne convention.
est_vide()etest_pleine():- Similaires à la pile bornée, basées sur
self.nb_elements.
- Similaires à la pile bornée, basées sur
ajouter(self, e):- On vérifie si la file est pleine.
- L’indice où le nouvel élément doit être ajouté est calculé par
(self.premier_indice + self.nb_elements) % self.capacite.self.premier_indice + self.nb_elementste donne l’indice « logique » si le tableau était infini.- Le
% self.capacitele « ramène » au début du tableau si l’indice dépasse la fin, simulant ainsi la circularité.
- On place
eà cetindice_ajout. - On incrémente
self.nb_elements.
retirer(self):- On vérifie si la file est vide.
- On récupère la valeur de l’élément à l’indice
self.premier_indice. - Optionnel :
self.tableau[self.premier_indice] = Nonepour libérer la référence. - Crucial : On met à jour
self.premier_indiceen le faisant avancer d’une position de manière circulaire :self.premier_indice = (self.premier_indice + 1) % self.capacite. - On décrémente
self.nb_elements. - On renvoie la valeur retirée.
consulter_premier(self):- Accède simplement à
self.tableau[self.premier_indice].
- Accède simplement à
Toutes les opérations de la file bornée implémentée ainsi ont une complexité en temps constant, mathcalO(1). C’est le moyen le plus efficace d’implémenter une file avec un tableau, sans avoir à déplacer tous les éléments à chaque retrait (ce qui serait mathcalO(N)).
Exercice 22 : Simulation d’Attente aux Guichets
Énoncé
Dans cet exercice, on se propose d’évaluer le temps d’attente de clients à des guichets, en comparant la solution d’une unique file d’attente et la solution d’une file d’attente par guichet.
Modélisation :
- Le temps est modélisé par une variable globale
horloge_globale, incrémentée à chaque tour de boucle. - Quand un nouveau client arrive, il est placé dans une file sous la forme d’un entier égal à la valeur de l’horloge (son heure d’arrivée).
- Quand un client est servi (sort de sa file), son temps d’attente est
horloge_globale - heure_arrivée_client. - On totalise le nombre de clients servis et le temps d’attente cumulé pour calculer le temps d’attente moyen.
Simulation des guichets :
- On se donne un nombre
N_GUICHETS(par exemple, 5). - Pour simuler la disponibilité d’un guichet, on utilise un tableau
disponibilite_guichetsde tailleN_GUICHETS.disponibilite_guichets[i]indique le nombre de tours d’horloge où le guichetisera occupé. Quand cette valeur vaut0, le guichet est libre. - Quand un client est servi par le guichet
i, on choisit un temps de traitement pour ce client au hasard entre0etN_GUICHETS(inclus), et on l’affecte àdisponibilite_guichets[i]. - À chaque tour d’horloge, on réalise deux opérations :
- On fait apparaître un nouveau client.
- Pour chaque guichet
i:- S’il est disponible (
disponibilite_guichets[i] == 0), il sert un nouveau client (pris dans sa propre file ou dans l’unique file, selon le modèle). - Sinon, on décrémente
disponibilite_guichets[i].
- S’il est disponible (
Mission : Écris un programme qui effectue une telle simulation, sur 100 000 tours d’horloge, et affiche au final le temps d’attente moyen. Compare avec différentes stratégies (unique file vs. une file par guichet, et pour plusieurs files : choix aléatoire ou choix de la file la plus courte).
Prérequis
- Avoir fait l’Exercice 21 (File Bornée), ou au moins comprendre bien le concept de file. Pour simplifier, tu peux utiliser les listes natives de Python comme des files (
appendpour ajouter,pop(0)pour retirer), mais une vraie implémentation de file est préférable pour la performance à grande échelle. - Utiliser des boucles.
- Générer des nombres aléatoires (
randommodule). - Calculer des moyennes.
Proposition de correction
Python
import random
# Réutilisation d'une classe File simple (listes Python pour faciliter l'exercice)
# Pour une vraie simulation à grande échelle, la FileBornee serait mieux.
class FileSimple:
def __init__(self):
self.elements = []
def est_vide(self):
return len(self.elements) == 0
def ajouter(self, e):
self.elements.append(e)
def retirer(self):
if self.est_vide():
raise IndexError("retirer d'une file vide")
return self.elements.pop(0) # pop(0) est O(N) mais suffisant pour la démo
def taille(self):
return len(self.elements)
# --- Paramètres de la simulation ---
N_GUICHETS = 5
DUREE_SIMULATION = 100000 # Tours d'horloge
# --- Simulation 1 : Une seule file d'attente pour tous les guichets ---
def simuler_unique_file():
print("\n--- Simulation : Une seule file d'attente pour tous les guichets ---")
file_unique = FileSimple()
disponibilite_guichets = [0] * N_GUICHETS # Temps avant que le guichet soit libre
total_attente = 0
clients_servis = 0
for horloge_globale in range(DUREE_SIMULATION):
# 1. Apparition d'un nouveau client (son heure d'arrivée est l'horloge actuelle)
file_unique.ajouter(horloge_globale) # Le client arrive à l'heure 'horloge_globale'
# 2. Pour chaque guichet
for i in range(N_GUICHETS):
if disponibilite_guichets[i] == 0: # Guichet i est libre
if not file_unique.est_vide(): # Y a-t-il un client à servir ?
heure_arrivee_client = file_unique.retirer()
attente_client = horloge_globale - heure_arrivee_client
total_attente += attente_client
clients_servis += 1
# Le guichet devient occupé pour un temps aléatoire (entre 0 et N_GUICHETS)
disponibilite_guichets[i] = random.randint(0, N_GUICHETS)
else:
# Guichet occupé, décrémente son temps d'occupation
disponibilite_guichets[i] -= 1
print(f"Clients servis : {clients_servis}")
print(f"Temps d'attente cumulé : {total_attente}")
if clients_servis > 0:
temps_attente_moyen = total_attente / clients_servis
print(f"Temps d'attente moyen : {temps_attente_moyen:.2f}")
else:
print("Aucun client servi.")
# --- Simulation 2 : Une file d'attente par guichet (choix aléatoire) ---
def simuler_multi_files_aleatoire():
print("\n--- Simulation : Une file d'attente par guichet (choix aléatoire) ---")
files_guichets = [FileSimple() for _ in range(N_GUICHETS)] # Une liste de files
disponibilite_guichets = [0] * N_GUICHETS
total_attente = 0
clients_servis = 0
for horloge_globale in range(DUREE_SIMULATION):
# 1. Apparition d'un nouveau client
# Le client choisit un guichet au hasard pour sa file
guichet_choisi = random.randint(0, N_GUICHETS - 1)
files_guichets[guichet_choisi].ajouter(horloge_globale)
# 2. Pour chaque guichet
for i in range(N_GUICHETS):
if disponibilite_guichets[i] == 0: # Guichet i est libre
if not files_guichets[i].est_vide(): # Y a-t-il un client dans SA file ?
heure_arrivee_client = files_guichets[i].retirer()
attente_client = horloge_globale - heure_arrivee_client
total_attente += attente_client
clients_servis += 1
disponibilite_guichets[i] = random.randint(0, N_GUICHETS)
else:
disponibilite_guichets[i] -= 1
print(f"Clients servis : {clients_servis}")
print(f"Temps d'attente cumulé : {total_attente}")
if clients_servis > 0:
temps_attente_moyen = total_attente / clients_servis
print(f"Temps d'attente moyen : {temps_attente_moyen:.2f}")
else:
print("Aucun client servi.")
# --- Simulation 3 : Une file d'attente par guichet (choix de la file la plus courte) ---
def simuler_multi_files_plus_courte():
print("\n--- Simulation : Une file d'attente par guichet (choix de la file la plus courte) ---")
files_guichets = [FileSimple() for _ in range(N_GUICHETS)]
disponibilite_guichets = [0] * N_GUICHETS
total_attente = 0
clients_servis = 0
for horloge_globale in range(DUREE_SIMULATION):
# 1. Apparition d'un nouveau client
# Le client choisit la file la plus courte
min_taille = float('inf') # Infini pour trouver le minimum
indice_file_plus_courte = 0
for i in range(N_GUICHETS):
if files_guichets[i].taille() < min_taille:
min_taille = files_guichets[i].taille()
indice_file_plus_courte = i
files_guichets[indice_file_plus_courte].ajouter(horloge_globale)
# 2. Pour chaque guichet
for i in range(N_GUICHETS):
if disponibilite_guichets[i] == 0: # Guichet i est libre
if not files_guichets[i].est_vide(): # Y a-t-il un client dans SA file ?
heure_arrivee_client = files_guichets[i].retirer()
attente_client = horloge_globale - heure_arrivee_client
total_attente += attente_client
clients_servis += 1
disponibilite_guichets[i] = random.randint(0, N_GUICHETS)
else:
disponibilite_guichets[i] -= 1
print(f"Clients servis : {clients_servis}")
print(f"Temps d'attente cumulé : {total_attente}")
if clients_servis > 0:
temps_attente_moyen = total_attente / clients_servis
print(f"Temps d'attente moyen : {temps_attente_moyen:.2f}")
else:
print("Aucun client servi.")
# --- Exécution des simulations ---
print("Exercice 22 : Simulation d'Attente aux Guichets")
simuler_unique_file()
simuler_multi_files_aleatoire()
simuler_multi_files_plus_courte()
print("-" * 20)
Explication de la correction :
Cet exercice est une application concrète et passionnante des files pour la modélisation de systèmes réels.
- Classe
FileSimple: J’ai utilisé une version simplifiée de la classeFilebasée sur les listes Python. Pour une simulation plus exigeante en performance, il serait judicieux d’utiliser laFileBorneede l’exercice 21, carlist.pop(0)est coûteux enO(N). - Paramètres :
N_GUICHETSetDUREE_SIMULATIONsont configurables. - Boucle Principale de Simulation : Pour chaque
horloge_globale(chaque « tour de boucle » ou « unité de temps ») :- Arrivée d’un client : Un nouveau client est toujours ajouté à une file. Son « heure d’arrivée » est simplement la valeur actuelle de
horloge_globale. - Gestion des guichets : On parcourt chaque guichet
i.- Guichet libre (
disponibilite_guichets[i] == 0) :- S’il y a un client dans la file du guichet (ou dans la file unique), ce client est
retiré. - On calcule son temps d’attente (
horloge_globale - heure_arrivee_client). - On met à jour les totaux (
total_attente,clients_servis). - Le guichet devient occupé pour une durée aléatoire (
random.randint(0, N_GUICHETS)).
- S’il y a un client dans la file du guichet (ou dans la file unique), ce client est
- Guichet occupé (
disponibilite_guichets[i] > 0) :- On décrémente son temps d’occupation (
disponibilite_guichets[i] -= 1).
- On décrémente son temps d’occupation (
- Guichet libre (
- Arrivée d’un client : Un nouveau client est toujours ajouté à une file. Son « heure d’arrivée » est simplement la valeur actuelle de
- Stratégies de File :
simuler_unique_file():- Tous les clients arrivent dans une seule
file_unique. - Chaque guichet, s’il est libre, prend le prochain client de cette
file_unique.
- Tous les clients arrivent dans une seule
simuler_multi_files_aleatoire():- Les clients sont répartis aléatoirement entre les
N_GUICHETSfiles d’attente (une par guichet).random.randint(0, N_GUICHETS - 1)choisit la file. - Chaque guichet ne sert que les clients de sa propre file.
- Les clients sont répartis aléatoirement entre les
simuler_multi_files_plus_courte():- Les clients choisissent la
filequi a actuellement lemin_taille(la file la plus courte). C’est la stratégie la plus « intelligente » pour le client. - Comme précédemment, chaque guichet ne sert que les clients de sa propre file.
- Les clients choisissent la
- Résultats : À la fin de la simulation, on affiche le nombre total de clients servis et le temps d’attente moyen.
Comparaison des stratégies (résultats typiques) :
Tu remarqueras que :
- La file unique est généralement la plus efficace ! Pourquoi ? Parce qu’elle garantit qu’aucun guichet n’est inactif s’il y a des clients en attente, même si un guichet a sa propre file vide. Les ressources (guichets) sont utilisées de manière optimale. C’est l’équité pour le système.
- Les files multiples avec choix aléatoire sont les moins efficaces. Certains guichets peuvent être débordés tandis que d’autres sont inactifs avec des files courtes ou vides, car les clients ne peuvent pas passer d’une file à l’autre.
- Les files multiples avec choix de la plus courte se situent entre les deux. C’est un compromis qui améliore l’efficacité par rapport au choix aléatoire, mais n’atteint généralement pas l’optimum de la file unique car les clients restent « bloqués » dans la file qu’ils ont choisie.
Cette simulation est une illustration parfaite de la théorie des files d’attente et de la manière dont les choix de conception (ici, le nombre et la gestion des files) peuvent avoir un impact majeur sur la performance d’un système. Et voilà, tu es désormais un pro des files d’attente… au moins en Python !
Ping : Terminale NSI 2025-26 – Maths & Informatique