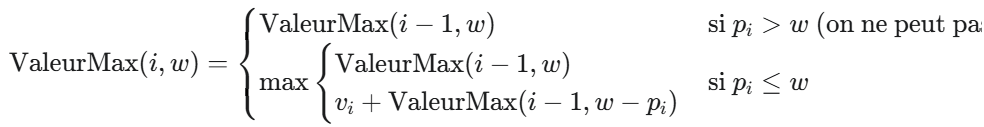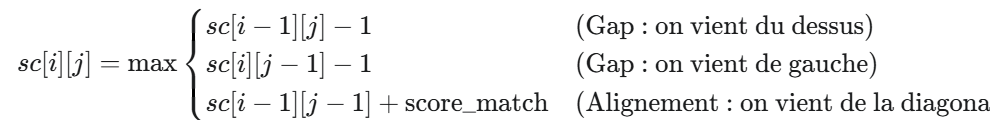activité

Corrigé de l’Exercice 1 : Le Problème de la Coupe de Barres d’Acier (Rod Cutting)

Ce problème vise à trouver le revenu maximal rn​ qu’on peut obtenir en coupant une barre de longueur n.

Exporter vers Sheets

Partie I : Analyse et Récursivité Naïve

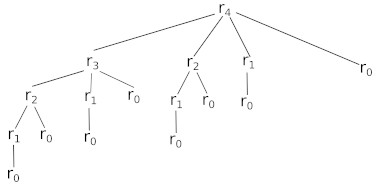
1. Exploration des possibilités pour n=4 :

Exporter vers Sheets

Le revenu maximum possible pour une barre de 4 m est de r4​=10€ (obtenu par la découpe 2+2).

2. Retrouver r4​ avec la Relation de Récurrence :

La relation est rn​=max(pn​,r1​+rn−1​,r2​+rn−2​,…,rn−1​+r1​). On utilise la forme simplifiée : rn​=max1≤i≤n​(pi​+rn−i​), avec r0​=0.

Pour n=4, on a :

r4​=max(p1​+r3​, p2​+r2​, p3​+r1​, p4​+r0​)r4​=max(1+8, 5+5, 8+1, 9+0)r4​=max(9, 10, 9, 9)=10

3. Compléter la Fonction Récursive (Naïve) :

La fonction implémente la relation rn​=max1≤i≤n​(pi​+rn−i​). Le terme manquant dans la boucle est la valeur récursive du reste de la barre : revenu_barre(n-i).

Python

def revenu_barre(n):    
   prix = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # Indice 0 inutilisé
   if n == 0:
        return 0 # Cas de base: revenu pour une barre de longueur 0 est 0
    
   r = float('-inf')
   for i in range(1, n + 1):
       # r = max(r, prix[longueur_du_premier_morceau] + revenu_max_du_reste)
       r = max(r, prix[i] + revenu_barre(n - i)) 
   return r

4. Application des Tarifs Initiaux :

En exécutant la fonction revenu_barre(n) avec les tarifs initiaux :

• r5​=13€ (Découpe : 2+3 ou 3+2)
• r6​=17€ (Découpe : 6 entier)
• r7​=18€ (Découpe : 1+6 ou 6+1)
• r8​=22€ (Découpe : 2+6 ou 6+2)
• r9​=25€ (Découpe : 1+8 ou 8+1)
• r10​=30€ (Découpe : 10 entier)

5. Changement de Tarifs :

Le tableau prix doit être mis à jour. Nouvelle liste des prix : prix = [0, 1, 6, 9, 11, 12, 19, 20, 23, 24, 26]

En réexécutant la fonction avec les nouveaux prix :

• r5​=15€ (Découpe : 2+3)
• r6​=19€ (Découpe : 6 entier)
• r7​=21€ (Découpe : 1+6 ou 6+1)
• r8​=25€ (Découpe : 2+6 ou 6+2)
• r9​=28€ (Découpe : 3+6 ou 6+3)
• r10​=31€ (Découpe : 2+8 ou 8+2)

Partie II : Optimisation par Programmation Dynamique

6. Approche Descendante (Mémorisation) :

On utilise un tableau mem pour stocker les résultats et éviter de recalculer rk​.

Python

def revenu_barre_dyn_desc(n):
    prix = [0, 1, 6, 9, 11, 12, 19, 20, 23, 24, 26]
    mem = [-1] * (n + 1) # -1 indique que le revenu n'a pas encore été calculé
    
    def r_mem(k):
        if k == 0:
            return 0
        
        # 1. Vérification : Si déjà calculé, retourner le résultat mémorisé
        if mem[k] != -1:
            return mem[k]
        
        # 2. Calcul : Sinon, calculer le revenu maximal
        r_max = float('-inf')
        for i in range(1, k + 1):
            # Utiliser r_mem(k - i) pour l'appel récursif (mémorisé)
            r_max = max(r_max, prix[i] + r_mem(k - i))
        
        # 3. Mémorisation : Stocker le résultat avant de le retourner
        mem[k] = r_max
        return r_max
        
    return r_mem(n)

7. Approche Ascendante (Itérative) :

On construit le tableau des revenus maximaux tab de bas en haut, de r1​ à rn​.

Python

def revenu_barre_dyn_asc(n):
    prix = [0, 1, 6, 9, 11, 12, 19, 20, 23, 24, 26]
    tab = [0] * (n + 1) # tab[i] stockera le revenu maximal ri
    # tab[0] est déjà à 0 (r0 = 0)
    
    # On itère de la longueur m=1 à m=n
    for m in range(1, n + 1):
        r_max = float('-inf')
        # On calcule le revenu maximal pour la longueur m
        for i in range(1, m + 1):
            # Calcul r_max = max(pi + r_m-i)
            # tab[m-i] contient le revenu r_m-i déjà calculé
            r_max = max(r_max, prix[i] + tab[m - i]) 
            
        tab[m] = r_max
        
    return tab[n]

Corrigé de l’Exercice 2 : Score Maximal dans une Pyramide de Nombres

Pyramides utilisées :

• ex1 = [[4],[6,2],[3,5,7],[5,1,6,2],[4,7,3,5,2]]
• ex2 = [[3],[1,2],[4,5,9],[3,6,2,1]]

Partie I : Représentation et Fonctions de Base

1. Dessiner la pyramide ex2 :

      [3]
     [1, 2]
    [4, 5, 9]
   [3, 6, 2, 1]

2. Dessiner le chemin ch2 = [0,1,2,2] dans ex2 :

Exporter vers Sheets

Le chemin est : 3→2→9→2.

3. Calculer le score de ch2 :

3+2+9+2=16

4. Fonction est_chemin(ch, p) :

Python

def est_chemin(ch, p):
    # Règle 1: La longueur doit correspondre au nombre de niveaux
    if len(ch) != len(p):
        return False
    
    # Règle 2: Doit commencer par 0
    if ch[0] != 0:
        return False
        
    # Règle 3: Vérification du déplacement
    for i in range(len(ch) - 1):
        a = ch[i]
        b = ch[i+1]
        
        # Le nouvel indice (b) doit être a ou a + 1
        if not (b == a or b == a + 1):
            return False
            
    # Si toutes les règles sont respectées
    return True

# Tests :
# est_chemin([0,1,2,2], ex2) -> True
# est_chemin([0, 0, 0, 2], ex2) -> False (problème à l'étape 3, 0 -> 2)

5. Fonction score(ch, p) :

Python

def score(ch, p):
    s = 0
    # Parcourt chaque niveau (i) de la pyramide et l'indice (j) du chemin
    for i in range(len(p)):
        j = ch[i]
        s += p[i][j]
    return s

# Test :
# score([0,1,1,1,2], ex1) -> 4 + 2 + 5 + 1 + 3 = 15

Partie II : Programmation Dynamique pour l’Optimisation

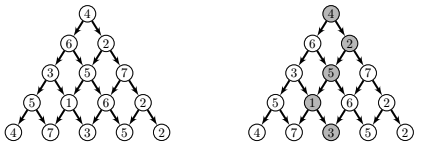
6. Fonction calcule_score_max(p) (Récursive Naïve) :

On utilise la relation récursive score_max(i,j)=p[i][j]+max(score_max(i+1,j),score_max(i+1,j+1)).

Python

def calcule_score_max(p, i=0, j=0):
    # Cas de base (dernier niveau)
    if i == len(p) - 1:
        return p[i][j]
    
    # Cas récursif: valeur du niveau courant + max des scores des deux sous-pyramides
    gauche = calcule_score_max(p, i + 1, j)
    droite = calcule_score_max(p, i + 1, j + 1)
    
    return p[i][j] + max(gauche, droite)

# Le score maximal est obtenu par calcule_score_max(ex1)

7. Fonction pyramide_nulle(n) :

La pyramide doit avoir n niveaux, avec i+1 éléments au niveau i.

Python

def pyramide_nulle(n):
    pyramide = []
    for i in range(n):
        # Chaque niveau i a une taille de i + 1
        pyramide.append([0] * (i + 1)) 
    return pyramide

# Exemple: pyramide_nulle(4) -> [[0],[0,0],[0,0,0],[0,0,0,0]]

8. Fonction prog_dyn(p) (Ascendante) :

On remplit la pyramide des scores s de bas en haut (du dernier niveau au sommet).

Python

def prog_dyn(p):
    n = len(p)
    if n == 0:
        return 0
        
    # Création de la pyramide des scores maximaux (s)
    # L'approche ascendante utilise souvent un tableau de la taille des données d'entrée.
    # Pour simplifier, on peut initialiser s avec la structure de p (ou une copie)
    s = [list(niveau) for niveau in p] 
    
    # On commence par l'avant-dernier niveau et on remonte jusqu'au sommet (niveau 0)
    for i in range(n - 2, -1, -1):
        # Pour chaque élément (j) du niveau i
        for j in range(len(s[i])):
            
            # Application de la relation de récurrence (score_max)
            # p[i][j] + max(score_max(i+1, j), score_max(i+1, j+1))
            
            # Les valeurs score_max(i+1, ...) sont déjà calculées au niveau i+1 de s.
            max_suivants = max(s[i+1][j], s[i+1][j+1])
            
            # Mise à jour du score maximal pour l'élément (i, j)
            s[i][j] = p[i][j] + max_suivants
            
    # Le score maximal pour la pyramide entière est au sommet
    return s[0][0]

# Test : prog_dyn(ex1) -> 4 + max(6, 2) + ... -> 23

9. Ordre de grandeur du coût de prog_dyn(p) :

La fonction prog_dyn(p) effectue deux boucles imbriquées :

1. La boucle extérieure parcourt les niveaux, de i=n−2 à 0 (soit ≈n niveaux).
2. La boucle intérieure parcourt les éléments j à chaque niveau. Au niveau i, il y a i+1 éléments.

Le nombre total d’opérations est proportionnel à la somme du nombre d’éléments dans la pyramide :

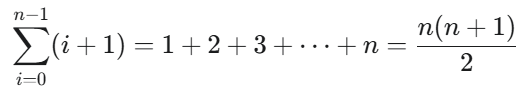
Le coût est donc dominé par n2. L’ordre de grandeur du coût est O(n2) (où n est le nombre de niveaux), ce qui est bien plus performant que l’approche récursive naïve en O(2n).

exercices

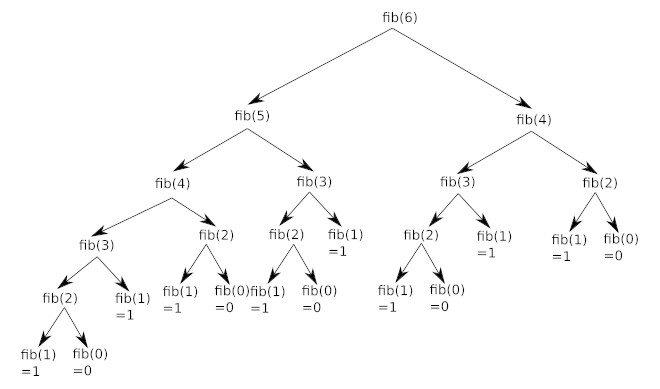
Exercice 1 Appels Redondants

Analyse des Appels Récursifs : L’exécution de rendu_monnaie([1, 2], 3) génère la séquence d’appels suivante :

1. rendu_monnaie(..., 3)
   • Appelle rendu_monnaie(..., 3 - 1 = 2)
   • Appelle rendu_monnaie(..., 3 - 2 = 1)
2. rendu_monnaie(..., 2)
   • Appelle rendu_monnaie(..., 2 - 1 = 1)
   • Appelle rendu_monnaie(..., 2 - 2 = 0)
3. rendu_monnaie(..., 1)
   • Appelle rendu_monnaie(..., 1 - 1 = 0)
4. rendu_monnaie(..., 0) → Retourne 0
5. rendu_monnaie(..., 1) (Appelé depuis s=2)
   • Appelle rendu_monnaie(..., 1 - 1 = 0)
6. rendu_monnaie(..., 0) → Retourne 0
7. rendu_monnaie(..., 0) → Retourne 0

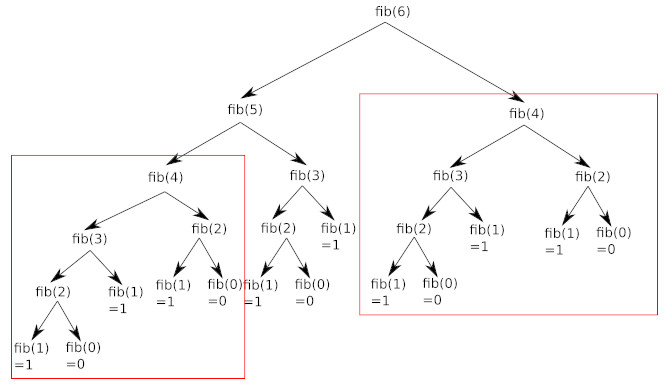
Conclusion sur la Redondance : Sur les 7 appels totaux (en comptant le premier), on constate que :

• Le sous-problème pour la somme s=1 a été calculé 2 fois.
• Le sous-problème pour la somme s=0 a été calculé 3 fois.

Ceci illustre le principe des sous-problèmes qui se chevauchent, caractéristique des problèmes résolus par Programmation Dynamique.

.

Corrigé 2 : Calcul du Tableau nb

Système de pièces : P={1,6,10}. Somme finale : S=12. Le tableau nb a une taille S+1=13 (indices 0 à 12). nb[0]=0.

Exporter vers Sheets

Tableau Final nb :

[0,1,2,3,4,5,1,2,3,4,1,2,2]

Le résultat final est nb[12]=2 (par exemple, 6+6 ou 10+2).

.

Corrigé 3 : Code Python avec Solution

Pour suivre la solution optimale, nous ajoutons un deuxième tableau, sol, qui mémorise la liste des pièces pour chaque somme n. Lorsque nous trouvons un meilleur score (1 + nb[n - p] < nb[n]), nous mettons à jour la solution en copiant la solution du sous-problème (sol[n - p]) et en lui ajoutant la pièce p qui a permis cette amélioration.

Python

def rendu_monnaie_solution(pieces, s):
    """
    Renvoie la liste minimale de pièces pour faire la somme s 
    avec le système 'pieces' (Programmation Dynamique).
    """
    # Initialisation au pire cas (n pièces de 1)
    nb = [n for n in range(s + 1)]          # Nombre minimal de pièces
    sol = [[1] * n for n in range(s + 1)] # Liste des pièces utilisées pour chaque somme
    sol[0] = []

    for n in range(1, s + 1):
        for p in pieces:
            if p <= n:
                # Si prendre la pièce p mène à un meilleur nombre total de pièces
                if 1 + nb[n - p] < nb[n]:
                    nb[n] = 1 + nb[n - p]
                    
                    # Mise à jour de la solution : 
                    # Prendre la solution optimale pour le reste (n-p) et ajouter la pièce p
                    sol[n] = sol[n - p].copy() 
                    sol[n].append(p)
                    
    # Retourne la solution optimale pour la somme s
    return sol[s]

Corrigé 4 : Code Python pour Fibonacci

La solution utilise un tableau f pour stocker toutes les valeurs F0​,F1​,…,Fn​ et les calculer de manière itérative, de bas en haut.

Python

def fibonacci(n):
    if n < 0:
        raise ValueError("n doit être positif")
    if n == 0:
        return 0
    
    # Création du tableau de mémorisation F[0] à F[n]
    f = [0] * (n + 1)
    
    # Initialisation des cas de base
    # f[0] = 0 (déjà fait par l'initialisation)
    f[1] = 1
    
    # Calcul itératif de F[2] jusqu'à F[n]
    for i in range(2, n + 1):
        # f[i] = f[i-2] + f[i-1] (Approche ascendante)
        f[i] = f[i - 2] + f[i - 1]
        
    return f[n]

Corrigé 5 : Tableau des Scores d’Alignement

Mots : s1​= »CHAT » (n1​=4) et s2​= »CAT » (n2​=3).

Calculs clés :

• sc[1][1] (C vs C) : max(−1+sc[0][1],−1+sc[1][0],1+sc[0][0])max(−1−1,−1−1,1+0)=max(−2,−2,1)=1
• sc[2][2] (H vs A) : max(−1+sc[1][2],−1+sc[2][1],−1+sc[1][1])max(−1+0,−1+0,−1+1)=max(−1,−1,0)=0
• sc[4][3] (T vs T) : max(−1+sc[3][3],−1+sc[4][2],1+sc[3][2])max(−1+0,−1+0,1+1)=max(−1,−1,2)=2

Le score maximal d’alignement (valeur dans la dernière case) est 2. (Un alignement optimal est : CH-AT contre C-AT, score 1−1+1+1=2).

Corrigé 6 : Alignement AAAAAAAAAA vs BBBBBBBBBB

Score Maximal : Puisque tous les caractères sont différents, il n’y a aucun match possible. Chaque paire alignée (A,B) est un mismatch avec un score de −1. Un alignement optimal sera l’un des deux suivants :

1. 10 Mismatchs : Score 10×(−1)=−10.
2. Gaps : L’alignement sera au maximum 10×(−1)=−10.

Le score maximal est −10.

Forme du Tableau (sc) : Le tableau sc a une taille 11×11.

Explication de la Forme :

• Bords (Ligne 0 et Colonne 0) : Remplis par les scores de gap : −i ou −j.
• Intérieur : Pour chaque case sc[i][j], la valeur est max(−1+sc[i−1][j],−1+sc[i][j−1],−1+sc[i−1][j−1]).
  • La meilleure option est toujours de prolonger l’alignement existant ou de le commencer.
  • La valeur sc[i][j] est max(sc[i−1][j],sc[i][j−1],sc[i−1][j−1])−1.
  • La structure triangulaire de −i sur la diagonale supérieure puis −j sur la diagonale inférieure n’est pas correcte. En réalité, le score sera simplement −max(i,j), car on peut toujours aligner la partie la plus courte avec des gaps et terminer avec des mismatchs. Dans ce cas particulier, sc[i][j]=−max(i,j).

(La correction fournie dans l’énoncé original semble contenir une erreur dans sa description de la structure générale du tableau pour ce cas).

Corrigé 7 : Fonction d’Affichage Formattée

La fonction utilise la méthode de formatage {:>3} pour assurer que chaque élément (caractère ou score) occupe exactement 3 espaces, aligné à droite.

Python

def affiche(s1, s2, sc):
    """Affiche la table des scores d'alignement de manière formattée."""
    
    # 1. Affichage de l'en-tête de colonne (s2)
    print(" ", end="") # Espace pour l'angle supérieur gauche
    for c in s2:
        print('{:>3}'.format(c), end="")
    print() # Retour à la ligne pour le début du tableau
    
    # 2. Affichage des lignes (s1 et scores)
    for i in range(len(sc)): # i va de 0 à len(s1)
        
        # Affichage du caractère de début de ligne (s1[i-1] ou espace/tirets pour la ligne 0)
        if i > 0:
            print('{:>3}'.format(s1[i - 1]), end="")
        else:
            print(" ", end="") # Espace pour la première ligne (index 0)

        # Affichage des scores de la ligne
        for v in sc[i]:
            print('{:>3}'.format(v), end="")
        print() # Retour à la ligne pour la ligne suivante
        
# Exemple d'utilisation (avec les données de l'exercice 5) :
# s1 = "CHAT", s2 = "CAT", sc = [[0,-1,-2,-3],[-1,1,0,-1],[-2,0,0,0],[-3,-1,1,0],[-4,-2,0,2]]
# affiche(s1, s2, sc)
#     C  A  T
#   0 -1 -2 -3
# C -1  1  0 -1
# H -2  0  0  0
# A -3 -1  1  0
# T -4 -2  0  2

Corrigé 8 : Reconstruction de la Solution

Nous introduisons un deuxième tableau, sol, qui, pour chaque paire d’indices (i,j), stocke la meilleure séquence d’alignement trouvée jusqu’à cet état (s1​[0:i],s2​[0:j]).

Python

def aligne_solution(s1, s2):
    n1, n2 = len(s1), len(s2)
    sc = [[0] * (n2 + 1) for _ in range(n1 + 1)]
    # sol[i][j] stockera le couple (align_s1, align_s2) optimal jusqu'à s1[i-1], s2[j-1]
    sol = [[("", "")] * (n2 + 1) for _ in range(n1 + 1)]

    # Initialisation des bords (Gaps)
    for i in range(1, n1 + 1):
        sc[i][0] = -i
        sol[i][0] = (s1[0:i], "-" * i) # Alignement de s1[0:i] avec des gaps
    for j in range(1, n2 + 1):
        sc[0][j] = -j
        sol[0][j] = ("-" * j, s2[0:j]) # Alignement de s2[0:j] avec des gaps

    # Reste du tableau
    for i in range(1, n1 + 1):
        for j in range(1, n2 + 1):
            
            # Options possibles et leurs scores
            score_gap_s1 = -1 + sc[i - 1][j]           # Gap dans s2 (vertical)
            score_gap_s2 = -1 + sc[i][j - 1]           # Gap dans s1 (horizontal)
            
            # Match ou Mismatch
            sim_score = 1 if s1[i - 1] == s2[j - 1] else -1
            score_diag = sim_score + sc[i - 1][j - 1] # Diagonale

            # Détermination du score maximal et de la solution correspondante
            
            # 1. Initialisation avec le meilleur score connu (souvent un gap)
            s_max = score_gap_s1
            (x, y) = sol[i - 1][j]
            sol[i][j] = (x + s1[i - 1], y + "-") # Aligne s1[i-1] avec un gap

            # 2. Test du Gap dans s1
            if score_gap_s2 > s_max:
                s_max = score_gap_s2
                (x, y) = sol[i][j - 1]
                sol[i][j] = (x + "-", y + s2[j - 1]) # Aligne s2[j-1] avec un gap

            # 3. Test de la Diagonale (Match ou Mismatch)
            if score_diag > s_max:
                s_max = score_diag
                (x, y) = sol[i - 1][j - 1]
                sol[i][j] = (x + s1[i - 1], y + s2[j - 1]) # Aligne les deux caractères

            sc[i][j] = s_max

    # Retourne le score et le couple de chaînes alignées
    return sc[n1][n2], sol[n1][n2]

Corrigé 9 : Adaptation du Programme pour la Biologie

Représentation de la Matrice de Similarités : Le format le plus pratique est un dictionnaire imbriqué (un dictionnaire de dictionnaires), permettant un accès facile O(1) par caractère :

Python

sim = {
    'A': {'A': 10, 'G': -1, 'C': -3, 'T': -4},
    'G': {'A': -1, 'G': 7,  'C': -5, 'T': -3},
    'C': {'A': -3, 'G': -5, 'C': 9,  'T': 0},
    'T': {'A': -4, 'G': -3, 'C': 0,  'T': 8}
}
gap = -5 # Coût du gap

Modification du Programme 48 : On remplace le score fixe de −1 pour les gaps et le score conditionnel de ±1 pour la diagonale par les valeurs de gap et de la matrice sim.

Python

def aligne_custom(s1, s2, sim, gap):
    n1, n2 = len(s1), len(s2)
    sc = [[0] * (n2 + 1) for _ in range(n1 + 1)]

    # Initialisation des bords avec le coût de gap
    for i in range(1, n1 + 1):
        sc[i][0] = i * gap # -1 est remplacé par gap
    for j in range(1, n2 + 1):
        sc[0][j] = j * gap # -1 est remplacé par gap

    # Le reste
    for i in range(1, n1 + 1):
        for j in range(1, n2 + 1):
            
            # 1. Score de Gap dans s2 (déplacement vertical)
            score_gap_s2 = gap + sc[i - 1][j]
            
            # 2. Score de Gap dans s1 (déplacement horizontal)
            score_gap_s1 = gap + sc[i][j - 1]
            
            # 3. Score d'alignement (déplacement diagonal)
            # Utilisation de la matrice sim
            score_sim = sim[s1[i - 1]][s2[j - 1]] + sc[i - 1][j - 1]
            
            # Score maximal parmi les trois options
            sc[i][j] = max(score_gap_s1, score_gap_s2, score_sim)
            
    return sc[n1][n2]

Corrigé 10 : Dénombrement sur Grille

Ce problème est résolu par la relation de récurrence : le nombre de chemins pour atteindre une case (i,j) est la somme des chemins pour atteindre la case du dessus (i−1,j) et la case de gauche (i,j−1).

chemins(i,j)=chemins(i−1,j)+chemins(i,j−1)

Cas de base :

• Le nombre de chemins pour atteindre n’importe quelle case sur la première ligne (i=0) ou la première colonne (j=0) est toujours 1.

Python

def chemins(n, m):
    """
    Calcule le nombre de chemins de (0, 0) à (n, m) sur une grille, 
    avec déplacements uniquement à droite ou en bas.
    """
    # La grille aura (n+1) lignes et (m+1) colonnes
    grille = [[0] * (m + 1) for _ in range(n + 1)]
    
    # Initialisation des bords (Cas de base: 1 chemin pour atteindre n'importe quelle case de la bordure)
    for i in range(n + 1):
        grille[i][0] = 1
    for j in range(m + 1):
        grille[0][j] = 1
        
    # Remplissage de la grille par approche ascendante
    for i in range(1, n + 1):
        for j in range(1, m + 1):
            # Le nombre de chemins pour (i, j) est la somme des chemins depuis le haut et la gauche
            grille[i][j] = grille[i - 1][j] + grille[i][j - 1]
            
    return grille[n][m]

# Vérification : chemins(2, 2) = 6 (Comme mentionné en introduction)

Exercice 1 : Le Problème de la Coupe de Barres d’Acier (Rod Cutting)

Ce problème, inspiré du livre « Introduction to Algorithms, » vise à maximiser le revenu obtenu en coupant une barre d’acier de longueur n en morceaux plus petits.

Données tarifaires :

L’entreprise Sun & Steel peut vendre une barre entière ou la découper pour maximiser son revenu.

Partie I : Analyse et Récursivité Naïve

1) Exploration des possibilités pour n=4 : La barre de 4 m peut être coupée de plusieurs façons. Continuez la liste ci-dessous pour trouver toutes les combinaisons de découpes et déterminez le revenu maximum r4​ possible :

• Vente entière (4): 9€
• Découpe en 2 morceaux (2+2): 5+5=10€
• Découpe en 2 morceaux (1+3): 1+8=9€
• Découpe en 3 morceaux (1+1+2): 1+1+5=7€
• … Ajoutez les combinaisons manquantes (par ex. 1+1+1+1, 1+2+1, etc.)
  

2) Formulation de la Relation de Récurrence : Le revenu maximum rn​ pour une barre de longueur n peut être calculé en considérant toutes les premières coupes possibles. On coupe la barre de longueur n en un premier morceau de longueur i (vendu au prix pi​) et on optimise le revenu sur le morceau restant de longueur n−i (qui rapporte rn−i​).La relation de récurrence est donc : rn​=max​(pi​+rn−i​) où 1≤i≤n et r0​=0 (revenu pour une barre de longueur nulle).Utilisez cette relation pour retrouver la valeur de r4​ en utilisant les revenus maximaux déjà calculés : r1​=1,r2​=5,r3​=8.

r4​=max(p1​+r3​, p2​+r2​, p3​+r1​, p4​+r0​)

3) Implémentation Récursive (Naïve) : Complétez la fonction récursive ci-dessous, qui implémente directement la relation rn​=max1≤i≤n​(pi​+rn−i​).

def revenu_barre(n):
    prix = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30] # Indice 0 inutilisé, prix[1] = p1, etc.
    if n == 0:
        return … # Cas de base
    r = float('-inf') # Initialisation au minimum possible
    for i in range(1, n + 1):
        # i est la longueur du premier morceau coupé
        r = max(r, prix[i] + ...) # Terme récursif à ajouter
    return r

4) Application : Utilisez la fonction revenu_barre pour calculer les revenus maximaux r5​,r6​,r7​,r8​,r9​ et r10​.

5) Changement de Tarifs : Le nouveau tableau de prix est proposé dans le tableau proposé plus bas.
Modifiez le tableau prix dans la fonction revenu_barre et recalculez les revenus maximaux rn​ pour n allant de 5 à 10.

Partie II : Optimisation par Programmation Dynamique

L’approche récursive simple entraîne de nombreux recalculs inutiles (sous-problèmes qui se chevauchent).

Pour une barre de 4 m, l’arbre de calcul montre que r1​ est calculé 4 fois et r2​ est calculé 2 fois. La programmation dynamique permet d’éviter cette redondance.

6. Approche Descendante (Mémorisation) : Écrivez une fonction revenu_barre_dyn_desc(n) qui utilise la mémorisation (un tableau mem) pour stocker et réutiliser les valeurs de ri​ déjà calculées, évitant ainsi les appels récursifs redondants.
   • Indice : La structure sera similaire à fib_mem du cours. Le tableau mem stocke ri​. Avant tout appel récursif, vérifiez si mem[n] est déjà calculé.
7. Approche Ascendante (Itérative) : Écrivez une fonction revenu_barre_dyn_asc(n) qui utilise une méthode itérative (boucles) pour calculer ri​ séquentiellement, de r1​ à rn​, en stockant les résultats dans un tableau.
   • Indice : Initialisez un tableau tab de taille n+1 avec tab[0]=0. Utilisez une boucle for allant de m=1 à n pour calculer tab[m] en utilisant la relation de récurrence et les valeurs déjà présentes dans le tableau.

Exercice 2 : Score Maximal dans une Pyramide de Nombres

Ce problème consiste à trouver le chemin de score maximal en partant du sommet d’une pyramide et en descendant en choisissant, à chaque niveau, l’élément immédiatement à gauche ou à droite.

La pyramide est représentée par une liste de listes. Exemple : ex1 = [[4],[6,2],[3,5,7],[5,1,6,2],[4,7,3,5,2]]

En gris on peut lire un des chemins possibles (qui est loin d’être le plus long) son score sera : 4 + 2 + 5 + 1 + 3 = 15.

Partie I : Représentation et Fonctions de Base

1. Représentation : Dessinez la pyramide représentée par la liste de listes ex2 = [[3],[1,2],[4,5,9],[3,6,2,1]].
2. Chemins et Indices : Un chemin est représenté par la liste des indices choisis à chaque niveau. Par exemple, le chemin gris dans ex1 est ch1 = [0,1,1,1,2]. Dessinez le chemin ch2 = [0,1,2,2] dans la pyramide ex2.
3. Calcul du Score : Calculez le score du chemin ch2 = [0,1,2,2] dans la pyramide ex2.
4. Fonction de Validation : Écrivez une fonction est_chemin(ch, p) qui vérifie si une liste d’indices ch est un chemin valide dans la pyramide p. Les règles sont :
   • Doit commencer par 0 (ch[0] == 0).
   • La longueur de ch doit être égale au nombre de niveaux de p.
   • Chaque indice consécutif b (au niveau i+1) doit être a ou a+1 par rapport à l’indice précédent a (au niveau i).
   • Tests : est_chemin(ch2, ex2) doit renvoyer True. est_chemin([0, 0, 0, 2], ex2) doit renvoyer False.
5. Fonction de Score : Écrivez une fonction score(ch, p) qui prend un chemin valide et la pyramide, et renvoie le score total.
   • Test : score(ch1, ex1) doit renvoyer 15.

Partie II : Programmation Dynamique pour l’Optimisation

Le problème du chemin maximal présente une structure de sous-problèmes optimaux. Le chemin optimal de la pyramide entière est composé du sommet et du chemin optimal de l’une des deux sous-pyramides adjacentes.

Soit score_max(i,j) le score maximal possible à partir du nombre situé à l’indice j du niveau i.

Les relations sont :

• Cas de base (dernier niveau) : score_max(len(p)−1,j)=p[len(p)−1][j]
• Cas récursif : score_max(i,j)=p[i][j]+max(score_max(i+1,j),score_max(i+1,j+1))

6. Implémentation Récursive (Naïve) : Écrivez une fonction calcule_score_max(p) qui utilise directement la relation de récurrence pour trouver le score maximal score_max(0,0).
7. Préparation pour la PD : Écrivez une fonction pyramide_nulle(n) qui crée une structure de pyramide (liste de listes) de n niveaux, remplie de zéros. Cette pyramide servira de tableau de mémorisation.
8. Approche Ascendante (Programmation Dynamique) : Écrivez une fonction prog_dyn(p) qui calcule le score maximal en utilisant la programmation dynamique ascendante (du bas vers le haut).
   • Créez une pyramide de mémorisation s de la même taille que p.
   • Commencez par initialiser le dernier niveau de s avec les valeurs du dernier niveau de p.
   • Remontez itérativement niveau par niveau (de len(p)−2 jusqu’à 0), en appliquant la formule score_max(i,j).
   • Le résultat final sera s[0][0].
9. Analyse de Complexité : Déterminez l’ordre de grandeur du coût (complexité en temps) de la fonction prog_dyn(p) pour une pyramide à n niveaux (sachant que le nombre d’éléments au niveau i est i+1).

Exercice 1 : Analyse de la Récursivité Naïve (Rendu de Monnaie)

Objectif : Identifier l’inefficacité des algorithmes récursifs sans mémorisation.

Énoncé : Soit la fonction récursive rendu_monnaie qui calcule le nombre minimal de pièces pour une somme donnée, sans utiliser la programmation dynamique :

Python

def rendu_monnaie(pieces, s):
    """
    Renvoie le nombre minimal de pièces pour faire la somme s 
    avec le système 'pieces' (approche récursive naïve).
    """
    if s == 0:
        return 0
    
    r = s # Initialisation au pire cas (1+1+...+1)
    for p in pieces:
        if p <= s:
            r = min(r, 1 + rendu_monnaie(pieces, s - p))
    return r

Question : Explicitez (à la main) tous les appels récursifs effectués par la fonction lorsque vous exécutez rendu_monnaie([1, 2], 3). Identifiez clairement les calculs redondants (les sous-problèmes qui sont résolus plusieurs fois).

Exercice 2 : Rendu de Monnaie par Programmation Dynamique (Ascendante)

Objectif : Comprendre le remplissage du tableau de mémorisation dans l’approche ascendante (Bottom-up).

Énoncé : Soit le programme d’approche ascendante (Programmation Dynamique) pour le rendu de monnaie :

Python

def rendu_monnaie(pieces, s):
    """
    Renvoie le nombre minimal de pièces pour faire la somme s 
    avec le système 'pieces' (approche dynamique ascendante).
    """
    nb = [0] * (s + 1) # Tableau de mémorisation
    
    for n in range(1, s + 1):
        nb[n] = n # Initialisation au pire cas (1+1+...+1)
        for p in pieces:
            if p <= n:
                # Mise à jour: 1 + nb[n - p] est le nombre de pièces si on prend la pièce p
                nb[n] = min(nb[n], 1 + nb[n - p])
    return nb[s]

Question : Calculez à la main et présentez l’état final du tableau nb lorsque l’on exécute rendu_monnaie([1, 6, 10], 12).

Exercice 3 : Rendu de Monnaie avec Solution Optimale

Objectif : Étendre l’approche dynamique pour tracer et reconstruire la solution (les pièces utilisées).

Énoncé : Modifiez le programme rendu_monnaie de l’Exercice 2 pour qu’il renvoie non seulement le nombre minimal de pièces, mais aussi la liste exacte des pièces qui composent cette solution optimale. Vous pouvez vous inspirer de l’exemple fourni (rendu_monnaie_solution).

Exercice 4 : Suite de Fibonacci par Programmation Dynamique

Objectif : Appliquer la PD à la suite de Fibonacci en utilisant l’approche ascendante (itérative).

Énoncé : La suite de Fibonacci est définie par F0​=0,F1​=1 et Fn​=Fn−1​+Fn−2​ pour n≥2. Écrivez une fonction fibonacci(n) qui calcule la valeur de Fn​ en utilisant la programmation dynamique (approche itérative, sans récursion).

voici un programme d’alignement de séquences fondamental sur lequel vont venir s’appuyer les exercices à suivre

def aligne(s1, s2):
    """le score du meilleur alignement de s1 et s2"""
    n1, n2 = len(s1), len(s2)
    sc = [[0] * (n2 + 1) for _ in range(n1 + 1)]
    # première ligne et première colonne
    for i in range(1, n1 + 1):
        sc[i][0] = -i
    for j in range(1, n2 + 1):
        sc[0][j] = -j
    # le reste
    for i in range(1, n1 + 1):
        for j in range(1, n2 + 1):
            s = max(-1 + sc[i - 1][j], -1 + sc[i][j - 1])
            if s1[i - 1] == s2[j - 1]:
                sc[i][j] = max(s, 1 + sc[i - 1][j - 1])
            else:
                sc[i][j] = max(s, -1 + sc[i - 1][j - 1])
    return sc[n1][n2]

Exercice 5 : Calcul du Tableau d’Alignement (Sequence Alignment)

Objectif : Appliquer manuellement la formule de récurrence du Programme 48 sur un petit exemple.

Énoncé : Le programme d’Alignement de Séquences (voir avant l’exercice 5) utilise la Programmation Dynamique pour calculer le score maximal d’alignement entre deux chaînes. Les règles de score utilisées par ce programme sont :

• Match : +1
• Mismatch : −1
• Gap (-) : −1

Question : Calculez à la main le tableau des scores d’alignement (sc) pour les deux mots « CHAT » et « CAT ». Quel est le score maximal final ?

Exercice 6 : Alignement de Séquences Identiques (Mismatchs)

Objectif : Déterminer la structure du tableau lorsque tous les alignements sont des mismatchs ou des gaps.

Énoncé : En utilisant les règles de score du programme d’Alignement de Séquences (voir avant l’exercice 5) (+1 pour match, -1 pour mismatch/gap), quel est le score maximal d’alignement des mots s1​= »AAAAAAAAAA » et s2​= »BBBBBBBBBB » (10 caractères chacun) ? Décrivez la forme du tableau calculé.

Exercice 7 : Affichage Formatté de la Table de Scores

Objectif : Créer une fonction utilitaire pour visualiser le tableau de Programmation Dynamique.

Énoncé : Écrivez une fonction affiche(s1, s2, sc) qui prend les deux séquences (s1, s2) et le tableau des scores (sc) calculé par le Programme 48, et affiche la table sous un format lisible et aligné.

Exercice 8 : Alignement avec Solution (Reconstruction)

Objectif : Modifier le programme d’alignement pour reconstruire la séquence d’opérations menant au score optimal.

Énoncé : Modifiez Le programme d’Alignement de Séquences (voir avant l’exercice 5) pour qu’il renvoie également la solution optimale sous la forme d’un couple de chaînes alignées (avec le caractère - pour les gaps).

Exercice 9 : Alignement avec Matrice de Similarités et Coût de Gap

Objectif : Généraliser le Programme 48 pour utiliser une matrice de similarités personnalisée et un coût de gap variable.

Énoncé : Dans les alignements biologiques (ADN), les scores ne sont pas fixes. Nous utilisons :

1. Une matrice de similarités (sim) pour le score d’alignement entre deux caractères spécifiques.
2. Une variable globale gap pour le coût de création d’un gap (-).

Question : Indiquez comment représenter la matrice de similarités en Python et modifiez le programme d’Alignement de Séquences (voir avant l’exercice 5) pour utiliser ces variables (sim et gap).

Exercice 10 : Nombre de Chemins sur une Grille

Objectif : Résoudre un problème de dénombrement par Programmation Dynamique.

Énoncé : Écrivez une fonction chemins(n, m) qui calcule le nombre de chemins possibles sur une grille de taille n×m (partant du coin supérieur gauche 0,0 jusqu’au coin inférieur droit n,m), en se déplaçant uniquement vers la droite ou vers le bas.

technique pour améliorer les Algorithmes Récursifs

La programmation dynamique est une puissante technique algorithmique qui transforme des solutions récursives « naïves » mais correctes en des solutions beaucoup plus efficaces en évitant les recalculs inutiles. Nous allons explorer cette méthode à travers un exemple classique, la suite de Fibonacci, et ensuite l’appliquer à un problème d’optimisation : le problème du sac à dos (Knapsack Problem).

1) La Suite de Fibonacci et le Recalcul Inutile

L’Approche Récursive Simple

La suite de Fibonacci (Fn​) est définie par F0​=0, F1​=1, et Fn​=Fn−1​+Fn−2​ pour n≥2. Une implémentation récursive directe en Python est la suivante :

Python

def fib_recursif(n):
    if n < 2:
        return n
    else:
        return fib_recursif(n-1) + fib_recursif(n-2)

Pour calculer F6​, l’exécution de ce code crée une structure arborescente d’appels. Si l’on déploie cet arbre pour F6​, on constate une forte redondance des calculs.

Par exemple, le calcul de F4​ est effectué deux fois, celui de F3​ est effectué trois fois, etc. Cette duplication des efforts entraîne une complexité temporelle qui augmente de manière exponentielle (O(2n)), rendant cette approche impraticable pour de grandes valeurs de n.

En observant attentivement le schéma ci-dessus, vous avez remarqué que de nombreux calculs sont inutiles, car effectués 2 fois : par exemple, on retrouve le calcul de fib(4) à 2 endroits (en haut à droite et un peu plus bas à gauche) :

L’Optimisation par Mémorisation (Approche Descendante)

L’idée fondamentale est d’éviter de recalculer un résultat une fois qu’il a été obtenu. Nous allons « mémoriser » la solution de chaque sous-problème (Fk​) dans un tableau ou un dictionnaire au fur et à mesure que nous le calculons.

Python

def fib_mem(n):
    # Initialise un tableau pour stocker les résultats.
    # Tous les résultats sont initialisés à 0 (ou une valeur "jamais calculée").
    memo = [0] * (n + 1)
    
    def f_mem(k):
        if k == 0 or k == 1:
            # Cas de base : on mémorise et retourne la valeur
            memo[k] = k
            return k
        
        # Vérification 1 : Si le résultat est déjà mémorisé, on le retourne directement.
        elif memo[k] > 0: # > 0 car F0=0 et on suppose n>0 pour les autres
            return memo[k]
        
        # Calcul : Si le résultat n'est pas mémorisé, on le calcule
        else:
            memo[k] = f_mem(k - 1) + f_mem(k - 2)
            return memo[k]
            
    return f_mem(n)

Principe de la Mémorisation :

1. Si la valeur de Fk​ a déjà été calculée (si elle est dans le tableau memo), on l’utilise sans faire de calcul supplémentaire.
2. Si la valeur de Fk​ n’a jamais été calculée, elle est calculée une unique fois, puis stockée dans le tableau memo pour une utilisation ultérieure.

Cette technique, appelée mémorisation (ou memoization), résout le problème Fk​ une seule fois, transformant la complexité exponentielle en une complexité beaucoup plus efficace, linéaire (O(n)). On parle ici de programmation dynamique descendante (top-down), car nous partons du problème principal (Fn​) et le décomposons jusqu’aux cas de base (F0​,F1​).

2) La Programmation Dynamique

a) Introduction et Concepts Fondamentaux

La Programmation Dynamique (PD) est une méthode algorithmique pour résoudre des problèmes complexes en les décomposant en sous-problèmes plus simples. Inventée par Richard Bellman dans les années 1950, le terme « programmation » est à prendre dans le sens de planification ou d’ordonnancement d’un processus, et non de codage.

La PD s’applique efficacement aux problèmes qui présentent deux caractéristiques principales :

1. Sous-problèmes Optimaux : Une solution optimale au problème principal doit être construite à partir de solutions optimales à ses sous-problèmes (principe de Bellman).
2. Sous-problèmes Réciproques (Overlapping Subproblems) : Les sous-problèmes se recoupent, c’est-à-dire que le même sous-problème est rencontré et doit être résolu plusieurs fois.

La PD résout chaque sous-problème une seule fois et mémorise sa réponse, évitant ainsi le coût du recalcul.

b) Approche Ascendante (Bottom-Up)

L’approche ascendante (ou bottom-up) est la deuxième facette de la programmation dynamique. Au lieu d’utiliser la récursivité et la mémorisation (descendante), elle utilise une approche itérative (boucles) pour construire la solution des plus petits sous-problèmes vers le problème principal.

Fibonacci avec l’Approche Ascendante

Pour Fibonacci, l’idée est de remplir le tableau des résultats en partant de F0​ et F1​ et en montant jusqu’à Fn​.

Python

def fib_asc(n):
    if n < 2:
        return n
        
    # Crée un tableau pour stocker F0, F1, ..., Fn
    tab = [0] * (n + 1)
    tab[1] = 1 # Initialise F1
    
    # Calcule F2, F3, ..., Fn de manière itérative
    for i in range(2, n + 1):
        tab[i] = tab[i - 1] + tab[i - 2]
        
    return tab[n]

Ce programme est très simple. On construit Fi​ à partir de Fi−1​ et Fi−2​ qui ont déjà été calculés et stockés dans le tableau tab. Chaque Fi​ est calculé une seule fois.

3) Application à l’Optimisation : Le Problème du Sac à Dos (Knapsack Problem 0/1)

Le problème du sac à dos (0/1) est un problème d’optimisation classique : Étant donné un sac à dos de capacité maximale W et une liste d’objets, chacun avec un poids pi​ et une valeur vi​, déterminer quels objets inclure dans le sac afin de maximiser la valeur totale sans dépasser la capacité W.

Ce problème ne peut pas être résolu de manière gloutonne (greedy) de manière fiable (par exemple, prendre toujours l’objet de plus grande valeur ou le meilleur rapport valeur/poids ne garantit pas la solution optimale globale).

Formulation Récursive et Sous-problèmes

Pour déterminer la valeur maximale que l’on peut obtenir avec une capacité w et les i premiers objets, nous avons deux choix pour l’objet i :

1. On inclut l’objet i : La valeur totale sera vi​ plus la valeur maximale obtenue avec la capacité restante w−pi​ et les i−1 premiers objets. (Possible seulement si pi​≤w).
2. On n’inclut pas l’objet i : La valeur totale sera la valeur maximale obtenue avec la capacité w et les i−1 premiers objets.

La relation de récurrence (pour un objet i de poids pi​ et valeur vi​, et une capacité w ) est :

Résolution par Programmation Dynamique Ascendante

Nous allons utiliser l’approche ascendante pour construire un tableau bidimensionnel DP, où DP[i][w] représente la valeur maximale que l’on peut obtenir en utilisant les i premiers objets pour une capacité de sac à dos w.

Exemple : Capacité W=5. Objets : O1​(p=2,v=3), O2​(p=3,v=4), O3​(p=4,v=5).

Exporter vers Sheets

Analyse du tableau :

• DP[1][2]: Pour w=2 et seul l’objet O1​ disponible. Puisque p1​=2≤2, DP[1][2]=max(DP[0][2],v1​+DP[0][2−2])=max(0,3+0)=3.
• DP[2][5]: Pour w=5 et les objets O1​,O2​ disponibles. Puisque p2​=3≤5, DP[2][5]=max(DP[1][5],v2​+DP[1][5−3])=max(3,4+DP[1][2]). DP[1][2]=3. Donc max(3,4+3)=7. (On prend O2​ et on utilise la meilleure valeur pour la capacité restante de 2 avec l’objet O1​).

La solution optimale est donnée par DP[N][W] (ici DP[3][5]=7). Le problème est résolu avec une complexité en temps de O(N×W), où N est le nombre d’objets et W la capacité maximale, bien plus efficace qu’une approche par force brute (tester toutes les combinaisons).

Coût vs Bénéfice

Comme pour Fibonacci, la programmation dynamique permet un gain spectaculaire en complexité temporelle (le temps d’exécution). Cependant, elle nécessite l’utilisation d’une structure de données (le tableau memo ou le tableau DP) pour stocker les résultats des sous-problèmes.

Conclusion : La programmation dynamique échange de l’efficacité en temps contre une augmentation de l’utilisation de la mémoire (complexité spatiale).

L’Alignement de Séquences : Le Détective de l’ADN 🕵️‍♀️

1. Le Problème : Comparer l’ADN (ou des Mots !)

Imaginez que vous êtes un détective et que vous avez deux longues chaînes de caractères (comme des brins d’ADN, ou simplement deux mots) que vous devez comparer pour voir à quel point elles sont similaires.

C’est le problème de l’Alignement de Séquences : comment mettre en face les caractères de deux chaînes pour maximiser les correspondances.

La Règle du Jeu : L’Alignement

Pour comparer deux mots (par exemple, « GENOME » et « ENORME »), nous allons les écrire l’un sous l’autre. Nous pouvons insérer des trous (représentés par un tiret, -) dans l’une ou l’autre chaîne.

• Contrainte essentielle : L’ordre des lettres ne doit jamais changer !
• Contrainte essentielle : On n’aligne jamais deux trous ensemble (-- est interdit).

Exporter vers Sheets

Comment Compter les Points (Le Score)

Pour trouver le « meilleur » alignement, on utilise un système de points simple :

Exporter vers Sheets

Exemple d’évaluation (GENO-ME vs -ENORME) :

Exporter vers Sheets

Score Total : (−1)+(+1)+(+1)+(+1)+(−1)+(+1)+(+1)=3

Le but de l’algorithme est de trouver l’alignement qui donne le score maximal possible.

2. L’Approche « Bête et Méchante » (Récursivité Naïve)

Comment un ordinateur chercherait-il la meilleure solution ?

Il pourrait essayer de le faire de manière récursive, c’est-à-dire en se ramenant à un problème plus petit à chaque étape.

La Décomposition Récursive

Pour trouver le meilleur score entre deux mots M1​ et M2​, il suffit de regarder leurs derniers caractères (c1​ et c2​). Il y a toujours trois choix possibles pour l’alignement final :

Exporter vers Sheets

Le Score Maximal pour M1​ et M2​ est simplement le maximum des scores obtenus par ces trois choix. On répète ensuite l’opération (récursion) sur les mots plus courts.

Le Problème des Recalculs (Pourquoi ça explose 💣)

Si on utilise cette approche, l’ordinateur va vite se retrouver à faire la même chose encore et encore.

Exemple : Pour aligner « GENOME » et « ENORME » :

1. Le Choix 1 vous demande d’aligner « GENOM » et « ENORM ».
2. Le Choix 2 vous demande d’aligner « GENOM » et « ENORME ».
3. Le Choix 3 vous demande d’aligner « GENOME » et « ENORM ».

Regardez le problème « GENOM » et « ENORM » : Il est calculé comme sous-problème dans les trois cas ! Ce problème est dit un sous-problème qui se chevauche.

Pour des mots de 20 lettres, ce phénomène de duplication se répète des milliards de fois, et le temps de calcul devient exponentiel (beaucoup trop lent !).

3. La Solution Intelligente : La Programmation Dynamique 🧠

Comme pour le problème du Rendu de Monnaie, nous allons utiliser la Programmation Dynamique (PD) pour éviter de recalculer les mêmes sous-problèmes. L’idée est de mémoriser chaque résultat.

Le Tableau de Scores (La « Carte »)

Au lieu de faire des appels récursifs et de tout oublier, nous allons construire un grand tableau à deux dimensions, appelé le tableau de scores (sc).

• Si le premier mot (s1​) a N lettres et le deuxième mot (s2​) a M lettres, le tableau aura une taille de (N+1)×(M+1).
• La case sc[i][j] va stocker le score maximal obtenu en alignant les i premières lettres de s1​ avec les j premières lettres de s2​.

Exporter vers Sheets

Le résultat que nous cherchons est toujours la case en bas à droite : sc[N][M].

L’Initialisation des Bords (Les Cas Simples)

On commence par remplir la première ligne et la première colonne (les cas où l’on aligne un mot avec un mot vide).

• sc[0][0]=0 : Aligner deux mots vides donne un score de 0.
• sc[i][0]=−i : Pour aligner les i premières lettres de s1​ avec un mot vide, nous devons faire i gaps (trous). Le coût est donc i×(−1)=−i.
• sc[0][j]=−j : De même, aligner s2​ avec un mot vide coûte −j.

Le Remplissage des Cases (Le Cœur du Calcul)

Pour remplir une case sc[i][j], nous utilisons la logique récursive des trois choix, mais au lieu d’appeler la fonction, nous regardons simplement les trois cases voisines qui ont déjà été calculées :

1. Voisin du Dessus (sc[i-1][j]) → Correspond au Choix 2 (Gap dans s2​).
2. Voisin de Gauche (sc[i][j-1]) → Correspond au Choix 3 (Gap dans s1​).
3. Voisin en Diagonale (sc[i-1][j-1]) → Correspond au Choix 1 (Alignement des deux derniers caractères s1​[i−1] et s2​[j−1]).

La formule de calcul (la relation de récurrence) devient :

Où score_match=+1 si s1​[i−1]=s2​[j−1], et −1 sinon.

L’Efficacité : Un Gain Incroyable 🚀

Grâce à cette méthode :

• Chaque case du tableau n’est calculée qu’une seule fois !
• Pour des mots de longueur N et M, le temps de calcul est proportionnel à la taille du tableau, soit N×M.

C’est une amélioration massive :

• Récursivité naïve : Temps exponentiel (O(2max(N,M))). Impraticable au-delà de 20 lettres.
• Programmation Dynamique : Temps polynomial (O(N×M)). C’est presque instantané même pour des séquences de milliers de caractères !

Ce tableau ne sert pas seulement à trouver le score maximal ; en remontant de la case finale à la case initiale en suivant les flèches du meilleur score à chaque fois, on peut reconstruire l’alignement optimal lui-même (comme vous le verrez dans certains exercices).

La méthode « Diviser pour régner » est un paradigme algorithmique puissant, souvent utilisé pour résoudre des problèmes complexes de manière élégante et efficace. L’idée est de décomposer un problème en plusieurs sous-problèmes, de les résoudre individuellement, puis de combiner leurs solutions pour obtenir la solution du problème initial.

Ce processus se décompose en trois phases principales :

• DIVISER : Le problème initial est scindé en plusieurs sous-problèmes plus petits, généralement de nature similaire à l’original.
• RÉGNER : Chaque sous-problème est résolu, souvent de manière récursive. La clé est que ces sous-problèmes sont plus simples à gérer que le problème de départ.
• COMBINER : Les solutions des sous-problèmes sont fusionnées pour construire la solution finale du problème d’origine.

Les algorithmes qui emploient cette approche sont très souvent de nature récursive. Un exemple classique de cette méthode est le tri-fusion.

Le Tri-Fusion

Présentation

Le tri-fusion est un algorithme de tri efficace qui repose sur le principe « Diviser pour régner ». Il prend un tableau non trié en entrée et renvoie le même tableau, mais cette fois, dans l’ordre croissant.

Voici une implémentation simplifiée en pseudo-code des deux fonctions qui composent cet algorithme : FUSION et TRI-FUSION.

VARIABLE
A : tableau d'entiers
L, R : tableaux d'entiers
p, q, r, n1, n2 : entiers
k, i, j : entiers

DEBUTFUSION (A, p, q, r):
    n1 ← q - p + 1
    n2 ← r - q
    créer tableau L[1..n1+1] et R[1..n2+1]
    pour i ← 1 à n1:
        L[i] ← A[p+i-1]
    fin pour
    pour j ← 1 à n2:
        R[j] ← A[q+j]
    fin pour
    L[n1+1] ← ∞
    R[n2+1] ← ∞
    i ← 1
    j ← 1
    pour k ← p à r:
        si L[i] ⩽ R[j]:
            A[k] ← L[i]
            i ← i + 1
        sinon:
            A[k] ← R[j]
            j ← j + 1
        fin si
    fin pour
fin FUSION

TRI-FUSION(A, p, r):
    si p < r:
        q = (p + r) / 2
        TRI-FUSION(A, p, q)
        TRI-FUSION(A, q+1, r)
        FUSION(A, p, q, r)
    fin si
fin TRI-FUSION

L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINER.

Un aspect intéressant du tri-fusion est que la phase de « Régner » est trivialement simple : le processus de division se poursuit jusqu’à ce que les sous-problèmes ne contiennent qu’un seul élément. Trier un tableau d’un seul élément ne demande aucune opération, ce qui simplifie grandement la tâche.

La véritable magie opère lors de la phase de fusion. Imaginons que nous ayons deux tableaux déjà triés, B et C, et que nous souhaitions les fusionner en un nouveau tableau T. On compare simplement le premier élément de B avec le premier de C, on ajoute le plus petit des deux à T, puis on recommence avec les éléments restants. On continue jusqu’à ce que l’un des tableaux soit vide, puis on ajoute les éléments restants de l’autre tableau à la fin de T.

Complexité

Bien que le calcul rigoureux soit hors de la portée de ce cours, nous pouvons en estimer la complexité de manière intuitive. La phase de division, où les tableaux sont coupés en deux à plusieurs reprises, est liée à la fonction logarithmique en base 2, soit log_2(n). La phase de fusion, pour un tableau de n éléments, nécessite un nombre de comparaisons proportionnel à n. En combinant ces deux observations, nous arrivons à une complexité approximative de l’ordre de O(nlog(n)).

Comme le montre la comparaison des courbes, un algorithme en O(nlog(n)) est beaucoup plus performant pour de grandes valeurs de n qu’un algorithme en O(n²), comme le tri par insertion ou le tri par sélection.

Retour sur la dichotomie

Présentation

C’est une méthode pour trouver un nombre N dans une liste triée si elle y est présente ou pour prouver son absence. Le principe est de regarder la valeur centrale, soit c’est celle qu’on cherche soit la valeur trouvée nous permettra de déterminer dans laquelle des sous listes de part et d’autre de la valeur devrait se situer N. Une fois fait on applique la même démarche sur la sous liste en question. On continuera jusqu’à soit tomber sur N ou obtenir une liste ne divise cette sous liste et on repère dans laquelle des parties devrait se situer la valeur. On continue, avec des sous listes de plus en plus petites et se dirigeant progressivement vers des listes vides. Soit on tombe sur N avant cela, sinon la valeur n’est pas présente. Cette recherche repose sur le principe « Diviser pour régner ».

exercice (corrigé ici)

compléter le code ci dessous

def recherche(t, v, g, d):
    """renvoie une position de v dans t[g..d],
    supposé trié, et None si elle ne s’y trouve pas"""
    if g > d:
        return None
    m = (g + d) // 2
    if t[m] < v:
        return recherche(t, v, m + 1, d)
    elif t[m] > v:
        return recherche(t, v, g, m - 1)
    else:
        return m

def recherche_dichotomique(t, v):
    """renvoie une position de v dans le tableau t,
    supposé trié, et None si elle ne s’y trouve pas"""
    return recherche(t, v, 0, len(t) - 1)

L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINE

Activités et Exercices

Activité 1

Appliquez l’algorithme de tri-fusion au tableau T= [23, 12, 4, 56, 35, 32, 42, 57, 3]. Vous pouvez créer un schéma et expliquer en détail la fusion de deux tableaux triés.

1. La phase de division

Le tri fusion commence par diviser de manière récursive le tableau initial en deux moitiés égales. Ce processus se poursuit jusqu’à ce que chaque sous-tableau ne contienne qu’un seul élément. À ce stade, le sous-tableau est considéré comme trié. C’est la partie « régner » de l’algorithme, qui est ici triviale.

2. La phase de fusion

Une fois que tous les sous-tableaux d’un seul élément sont formés, le tri fusion passe à la phase la plus importante : la fusion. L’idée est de fusionner deux sous-tableaux déjà triés en un seul grand tableau trié. C’est un processus simple qui se déroule en comparant les premiers éléments de chaque sous-tableau.

Prenons l’exemple de la fusion des deux tableaux triés suivants :

• B = [4, 12, 23, 35, 56]
• C = [3, 32, 42, 57]

Nous allons construire un nouveau tableau, T, qui contiendra le résultat de la fusion.

1. On compare le premier élément de B (4) avec le premier élément de C (3). Comme 3 est plus petit que 4, on le place dans T.
   • T = [3]
   • B = [4, 12, 23, 35, 56]
   • C = [32, 42, 57]
2. On compare à nouveau le premier élément restant de B (4) avec le premier élément de C (32). Comme 4 est plus petit, on le place dans T.
   • T = [3, 4]
   • B = [12, 23, 35, 56]
   • C = [32, 42, 57]
3. On continue ce processus :
   • On compare 12 et 32 : 12 est plus petit. On ajoute 12 à T.
   • On compare 23 et 32 : 23 est plus petit. On ajoute 23 à T.
   • On compare 35 et 32 : 32 est plus petit. On ajoute 32 à T.
   • On compare 35 et 42 : 35 est plus petit. On ajoute 35 à T.
   • On compare 56 et 42 : 42 est plus petit. On ajoute 42 à T.
   • On compare 56 et 57 : 56 est plus petit. On ajoute 56 à T.

À ce stade, le tableau B est vide. Il ne reste plus qu’un seul élément dans C (57). On l’ajoute directement à la fin du tableau T.

• Le tableau final trié est donc : T = [3, 4, 12, 23, 32, 35, 42, 56, 57].

Ce processus de comparaison et d’ajout est répété pour toutes les fusions successives jusqu’à ce que tous les éléments soient rassemblés dans un seul tableau final trié.

Activité 2

Complétez le code Python suivant pour la fonction de tri-fusion :

def tri_fusion(tab):
    def fusion(tab, p, q, r):
        n1 = q-p+1
        n2 = r-q
        L = [0]*n1
        R = [0]*n2
        for i in range(n1):
            L[i] = tab[p+i]
        for j in range(n2):
            R[j] = tab[q+j+1]
        L.append(float("inf"))
        R.append(float("inf"))
        i = 0
        j = 0
        for k in range(p, r+1):
            if L[i] <= R[j]:
                tab[k] = L[i]
                i = i + 1
            else:
                tab[k]=R[j]
                j = j + 1

    def tri_f(tab, p, r) :
        if p < r:
            q = (p + r) // 2
            tri_f(tab, p, q)
            tri_f(tab, q + 1, r)
            fusion(tab, p, q, r)

    tri_f(tab, p = 0, r = len(tab) - 1)
    return tab

Activité 3

Complétez cette autre version du tri-fusion en Python, en utilisant le « slicing » :

def tri_fusion_slice(tab):
    n = len(tab)
    if n > 1:
        mil = n // 2
        L = tab[:mil]
        R = tab[mil:]
        tri_fusion_slice(L)
        tri_fusion_slice(R)
        i = 0
        j = 0
        k = 0
        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                tab[k] = L[i]
                i += 1
            else:
                tab[k] = R[j]
                j += 1
            k += 1
        while i < len(L):
            tab[k] = L[i]
            i += 1
            k += 1
        while j < len(R):
            tab[k] = R[j]
            j += 1
            k += 1

Activité 4

En vous basant sur la vidéo disponible à cette adresse, implémentez l’algorithme de tri rapide (Quicksort) en Python, un autre algorithme basé sur le principe « Diviser pour régner ».

Exercices

• Exercice 1 : Donnez la séquence des appels à la fonction de recherche dichotomique du cours pour les appels recherche_dichotomique([0,1,1,2,3,5,8,13,21], 13) et recherche_dichotomique([0,1,1,2,3,5,8,13,21], 12).
• Exercice 2 : Quelles sont les deux listes renvoyées par une fonction coupe() à laquelle on passe la liste [8, 1, 3, 0, 1, 2, 5] ? L’ordre relatif est-il préservé ? Est-ce important ?
• Exercice 3 : Réécrivez la fonction fusion en utilisant une boucle while au lieu de la récursivité.
• Exercice 4 : Le problème des Tours de Hanoï est un jeu célèbre impliquant trois tiges et des disques de tailles différentes. Écrivez une fonction hanoi(n) qui affiche la solution pour n disques.
• Exercice 5 : Combien de déplacements élémentaires faut-il au total pour déplacer N disques de la tour de départ à la tour d’arrivée dans le problème des Tours de Hanoï ?
• Exercice 6 : Réécrivez l’exercice 4 en utilisant des piles (voir chapitre 5).
• Exercice 7 : Écrivez une fonction qui effectue la rotation d’une image de 90 degrés en utilisant le principe « Diviser pour régner ».
• Exercice 8 : Appliquez le principe « Diviser pour régner » pour multiplier deux entiers en utilisant la méthode de Karatsuba.

corrections

Exercice 1

• Pour recherche_dichotomique([0,1,1,2,3,5,8,13,21], 13) :
  • recherche(t, 13, 0, 8)
  • recherche(t, 13, 5, 8)
  • recherche(t, 13, 7, 8)
  • À ce moment, l’index m est 7, où se trouve la valeur 13.
• Pour recherche_dichotomique([0,1,1,2,3,5,8,13,21], 12) :
  • recherche(t, 12, 0, 8)
  • recherche(t, 12, 5, 8)
  • recherche(t, 12, 7, 8)
  • recherche(t, 12, 7, 6)
  • À ce moment, l’indice de gauche g est supérieur à l’indice de droite d, et la recherche se termine avec le résultat None.

Exercice 2

Les deux listes renvoyées sont [5, 1, 3, 8] et [2, 0, 1]. L’ordre relatif des éléments est inversé, car la fonction ajoute les éléments au début des nouvelles listes. Cependant, ce n’est pas important pour le tri-fusion, car les deux listes sont triées avant d’être fusionnées, ce qui annule l’inversion initiale.

Exercice 3

def fusion(l1, l2):
    lst = None
    while l1 is not None or l2 is not None:
        if l1 is not None and (l2 is None or l1.valeur <= l2.valeur):
            lst, l1 = Cellule(l1.valeur, lst), l1.suivante
        else:
            lst, l2 = Cellule(l2.valeur, lst), l2.suivante

    # Puis on inverse la liste lst
    r = None
    while lst is not None:
        r, lst = Cellule(lst.valeur, r), lst.suivante
    return r

Exercice 4

def deplace(a, b, c, k):
    """Déplace k disques de la tour a vers la tour b, en se servant de la tour c comme intermédiaire"""
    if k > 0:
        deplace(a, c, b, k - 1)
        print("déplace de", a, "vers", b)
        deplace(c, b, a, k - 1)

def hanoi(n):
    deplace(1, 3, 2, n)

Exercice 5

Pour déplacer $N$ disques, il faut au total $2^N - 1$ déplacements élémentaires. La preuve se fait par récurrence :
* Pour $N=1$, il faut $2^1 - 1 = 1$ déplacement.
* Si l'on suppose qu'il faut $2^{N-1} - 1$ déplacements pour $N-1$ disques, alors pour $N$ disques, on aura :
    * $2^{N-1} - 1$ déplacements pour déplacer les $N-1$ premiers disques de la tour de départ à la tour intermédiaire.
    * 1 déplacement pour le plus grand disque de la tour de départ à la tour d'arrivée.
    * $2^{N-1} - 1$ déplacements pour déplacer les $N-1$ disques de la tour intermédiaire à la tour d'arrivée.
    * Total : $(2^{N-1} - 1) + 1 + (2^{N-1} - 1) = 2 \times 2^{N-1} - 1 = 2^N - 1$.

Exercice 6

def hanoi_piles(n):
    a = Pile()
    for i in range(n, 0, -1):
        a.empiler(i)
    
    deplace(a, Pile(), Pile(), n)

def deplace(a, b, c, k):
    """déplace k disques de la pile a vers la pile b, en se servant de la pile c comme intermédiaire"""
    if k > 0:
        deplace(a, c, b, k - 1)
        b.empiler(a.depiler())
        deplace(c, b, a, k - 1)

Exercice 7

def rotation_aux(px, x, y, t):
    '''on va faire la rotation de l'image située entre les pixels de coordonnées (x,y) et (x+t,y+t)'''
    if t == 1:
        return
    
    t //= 2
    rotation_aux(px, x, y, t)
    rotation_aux(px, x + t, y, t)
    rotation_aux(px, x, y + t, t)
    rotation_aux(px, x + t, y + t, t)

    for x1 in range(x, x + t):
        for y1 in range(y, y + t):
            px[x1, y1 + t]=px[x1, y1]  
            px[x1 + t, y1 + t]= px[x1, y1 + t]
            px[x1 + t, y1]=  px[x1 + t, y1 + t]
            px[x1, y1] =px[x1 + t, y1]

def rotation(px, taille):
    rotation_aux(px, 0, 0, taille)

Exercice 8

voici deux version du programme en Python. Il faudra copier l’une ou l’autre (car les noms de fonctions sont les mêmes dans les deux versions)

#en base 10
def taille(x):
    n = 1
    while x > 0:
        x //= 10
        n += 1
    return n

def karatsuba(x, y, n):
    """multiplie x et y par la méthode de Karatsuba"""
    if n <= 1:
        return x * y

    n //= 2
    a, b = x // 10**n, x % 10**n
    c, d = y // 10**n, y % 10**n

    ac = karatsuba(a, c, n)
    bd = karatsuba(b, d, n)
    abcd = karatsuba(a - b, c - d, n)

    return (ac * 10 ** (2 * n)) + ((ac + bd - abcd) * 10**n) + bd

def mult(x, y):
    n = max(taille(abs(x)), taille(abs(y)))
    return karatsuba(x, y, n)

print(mult(2457,6819))


# en base 2



def taille(x):
    n = 1
    while x > 0:
        x //= 2
        n += 1
    return n

def karatsuba(x, y, n):
    """multiplie x et y par la méthode de Karatsuba"""
    if n <= 1:
        return x * y
    
    n //= 2
    m = 1 << n
    a, b = x >> n, x % m
    c, d = y >> n, y % m
    
    ac = karatsuba(a, c, n)
    bd = karatsuba(b, d, n)
    abcd = karatsuba(a - b, c - d, n)
    
    return (ac << (2 * n)) + ((ac + bd - abcd) << n) + bd

def mult(x, y):
    n = max(taille(abs(x)), taille(abs(y)))
    return karatsuba(x, y, n)

La méthode « Diviser pour régner » est un paradigme algorithmique puissant, souvent utilisé pour résoudre des problèmes complexes de manière élégante et efficace. L’idée est de décomposer un problème en plusieurs sous-problèmes, de les résoudre individuellement, puis de combiner leurs solutions pour obtenir la solution du problème initial.

Ce processus se décompose en trois phases principales :

• DIVISER : Le problème initial est scindé en plusieurs sous-problèmes plus petits, généralement de nature similaire à l’original.
• RÉGNER : Chaque sous-problème est résolu, souvent de manière récursive. La clé est que ces sous-problèmes sont plus simples à gérer que le problème de départ.
• COMBINER : Les solutions des sous-problèmes sont fusionnées pour construire la solution finale du problème d’origine.

Les algorithmes qui emploient cette approche sont très souvent de nature récursive. Un exemple classique de cette méthode est le tri-fusion.

Le Tri-Fusion

Présentation

Le tri-fusion est un algorithme de tri efficace qui repose sur le principe « Diviser pour régner ». Il prend un tableau non trié en entrée et renvoie le même tableau, mais cette fois, dans l’ordre croissant.

Voici une implémentation simplifiée en pseudo-code des deux fonctions qui composent cet algorithme : FUSION et TRI-FUSION.

VARIABLE
A : tableau d'entiers
L, R : tableaux d'entiers
p, q, r, n1, n2 : entiers
k, i, j : entiers

DEBUT
FUSION (A, p, q, r):
    n1 ← q - p + 1
    n2 ← r - q
    créer tableau L[1..n1+1] et R[1..n2+1]
    pour i ← 1 à n1:
        L[i] ← A[p+i-1]
    fin pour
    pour j ← 1 à n2:
        R[j] ← A[q+j]
    fin pour
    L[n1+1] ← ∞
    R[n2+1] ← ∞
    i ← 1
    j ← 1
    pour k ← p à r:
        si L[i] ⩽ R[j]:
            A[k] ← L[i]
            i ← i + 1
        sinon:
            A[k] ← R[j]
            j ← j + 1
        fin si
    fin pour
fin FUSION

TRI-FUSION(A, p, r):
    si p < r:
        q = (p + r) // 2
        TRI-FUSION(A, p, q)
        TRI-FUSION(A, q+1, r)
        FUSION(A, p, q, r)
    fin si
fin TRI-FUSION

visuellement ça donne ça :

L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINER.

Un aspect intéressant du tri-fusion est que la phase de « Régner » est trivialement simple : le processus de division se poursuit jusqu’à ce que les sous-problèmes ne contiennent qu’un seul élément. Trier un tableau d’un seul élément ne demande aucune opération, ce qui simplifie grandement la tâche.

La véritable magie opère lors de la phase de fusion. Imaginons que nous ayons deux tableaux déjà triés, B et C, et que nous souhaitions les fusionner en un nouveau tableau T. On compare simplement le premier élément de B avec le premier de C, on ajoute le plus petit des deux à T, puis on recommence avec les éléments restants. On continue jusqu’à ce que l’un des tableaux soit vide, puis on ajoute les éléments restants de l’autre tableau à la fin de T.

Complexité

Bien que le calcul rigoureux soit hors de la portée de ce cours, nous pouvons en estimer la complexité de manière intuitive. La phase de division, où les tableaux sont coupés en deux à plusieurs reprises, est liée à la fonction logarithmique en base 2, soit log_2(n). La phase de fusion, pour un tableau de n éléments, nécessite un nombre de comparaisons proportionnel à n. En combinant ces deux observations, nous arrivons à une complexité approximative de l’ordre de O(nlog(n)).

Comme le montre la comparaison des courbes, un algorithme en O(nlog(n)) est beaucoup plus performant pour de grandes valeurs de n qu’un algorithme en O(n²), comme le tri par insertion ou le tri par sélection.

Retour sur la dichotomie

Présentation

C’est une méthode pour trouver un nombre N dans une liste triée si elle y est présente ou pour prouver son absence. Le principe est de regarder la valeur centrale, soit c’est celle qu’on cherche soit la valeur trouvée nous permettra de déterminer dans laquelle des sous listes de part et d’autre de la valeur devrait se situer N. Une fois fait on applique la même démarche sur la sous liste en question. On continuera jusqu’à soit tomber sur N ou obtenir une liste ne divise cette sous liste et on repère dans laquelle des parties devrait se situer la valeur. On continue, avec des sous listes de plus en plus petites et se dirigeant progressivement vers des listes vides. Soit on tombe sur N avant cela, sinon la valeur n’est pas présente. Cette recherche repose sur le principe « Diviser pour régner ».

exercice (corrigé ici)

compléter le code ci dessous

def recherche(t, v, g, d):
    """renvoie une position de v dans t[g..d],
    supposé trié, et None si elle ne s’y trouve pas"""
    ...

def recherche_dichotomique(t, v):
    """renvoie une position de v dans le tableau t,
    supposé trié, et None si elle ne s’y trouve pas"""
    return ...

L’appel initial pour trier un tableau A est TRI-FUSION(A, 1, A.longueur). Notez que dans cet algorithme, la fonction TRI-FUSION gère la phase de DIVISER, tandis que la fonction FUSION combine les phases de RÉGNER et de COMBINE

Activités et Exercices

Activité 1

Appliquez l’algorithme de tri-fusion au tableau T= [23, 12, 4, 56, 35, 32, 42, 57, 3]. Vous pouvez créer un schéma et expliquer en détail la fusion de deux tableaux triés.

Activité 2

Complétez le code Python suivant pour la fonction de tri-fusion :

def tri_fusion(tab):

    # Fonction pour fusionner deux sous-tableaux triés
    def fusion(tab, p, q, r):
        n1 = q - p + 1
        n2 = r - q
        
        # On crée deux tableaux temporaires, L et R
        L = [0] * n1
        R = [0] * n2

        # On remplit les tableaux L et R
        for i in range(n1):
            L[i] = tab[p + i]
        for j in range(n2):
            R[j] = tab[q + j + 1]

        # On ajoute un 'sentinelle' (une valeur très grande) à la fin de chaque tableau
        # Cela nous permet d'éviter de vérifier si un tableau est vide
        L.append(float("inf"))
        R.append(float("inf"))
        
        i = 0  # Indice pour le tableau L
        j = 0  # Indice pour le tableau R
        
        # On parcourt le tableau original pour y placer les éléments triés
        for k in range(p, r + 1):
            if __________:  # Quelle est la condition pour savoir quel élément choisir ?
                tab[k] = L[i]
                i = i + 1
            else:
                tab[k] = R[j]
                j = j + 1

    # Fonction principale récursive pour le tri
    def tri_f(tab, p, r):
        # Quelle est la condition pour arrêter la récursion ?
        if __________:
            # On calcule le milieu
            q = _________
            
            # 1. On trie la première moitié du tableau
            tri_f(tab, p, q)
            
            # 2. On trie la deuxième moitié du tableau
            tri_f(tab, q + 1, r)
            
            # 3. On fusionne les deux moitiés triées
            fusion(tab, p, q, r)

    # Appel initial de la fonction de tri
    tri_f(tab, p=0, r=_________)  # De quelle borne à quelle borne allons-nous trier le tableau ?
    return tab

Activité 3

Complétez cette autre version du tri-fusion en Python, en utilisant le « slicing » :

def tri_fusion_slice(tab):
    n = len(tab)
    
    # Condition d'arrêt de la récursion
    if __________:  # Quand arrêtons-nous de diviser le tableau ?
        
        # Calcul du point milieu pour diviser le tableau
        mil = _________
        
        # On divise le tableau en deux sous-tableaux (slicing)
        L = tab[:mil]
        R = tab[mil:]
        
        # Appels récursifs pour trier chaque moitié
        tri_fusion_slice(L)
        tri_fusion_slice(R)
        
        # Indices pour parcourir les tableaux L, R et le tableau final
        i = 0  
        j = 0  
        k = 0  
        
        # Boucle principale de fusion : on compare et on place les éléments
        while i < len(L) and j < len(R):
            if __________:  # Quelle est la condition pour choisir l'élément de L ?
                tab[k] = L[i]
                i += 1
            else:
                tab[k] = R[j]
                j += 1
            k += 1
            
        # Boucles pour ajouter les éléments restants (s'il y en a)
        while i < len(L):
            tab[k] = L[i]
            i += 1
            k += 1
            
        while __________:  # Quelle est la condition pour ajouter les éléments restants de R ?
            tab[k] = R[j]
            j += 1
            k += 1

Activité 4

En vous basant sur la vidéo disponible à cette adresse, implémentez l’algorithme de tri rapide (Quicksort) en Python, un autre algorithme basé sur le principe « Diviser pour régner ».

Exercices

• Exercice 1 : Donnez la séquence des appels à la fonction de recherche dichotomique du cours pour les appels recherche_dichotomique([0,1,1,2,3,5,8,13,21], 13) et recherche_dichotomique([0,1,1,2,3,5,8,13,21], 12).
• Exercice 2 : Quelles sont les deux listes renvoyées par une fonction coupe() à laquelle on passe la liste [8, 1, 3, 0, 1, 2, 5] ? L’ordre relatif est-il préservé ? Est-ce important ?
• Exercice 3 : Réécrivez la fonction fusion en utilisant une boucle while au lieu de la récursivité.
• Exercice 4 : Le problème des Tours de Hanoï est un jeu célèbre impliquant trois tiges et des disques de tailles différentes. Écrivez une fonction hanoi(n) qui affiche la solution pour n disques.
• Exercice 5 : Combien de déplacements élémentaires faut-il au total pour déplacer N disques de la tour de départ à la tour d’arrivée dans le problème des Tours de Hanoï ?
• Exercice 6 : Réécrivez l’exercice 4 en utilisant des piles (voir chapitre 5).
• Exercice 7 : Écrivez une fonction qui effectue la rotation d’une image de 90 degrés en utilisant le principe « Diviser pour régner ». indications et voir photo plus bas.
• Exercice 8 : Appliquez le principe « Diviser pour régner » pour multiplier deux entiers en utilisant la méthode de Karatsuba.

🎲 Le Maître des Permutations 🤹‍♂️

Un problème classique et élégant à résoudre avec la récursivité est de générer toutes les permutations d’une liste (toutes les façons d’ordonner ses éléments).

Par exemple, pour [1, 2, 3], les permutations sont [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1].

Comment ça marche pour trouver les permutation des éléments d’une liste

1. On choisit un élément de la liste.
2. On identifie ce qui reste d’éléments à traiter
3. On lance un appel de notre fonction récursive pour générer une liste des permutations de ce qui reste d’éléments à traiter (autrement dit on crée un liste des permutations des éléments restants) cet appel peut en provoquer un autre qui en provoque un autre…jusqu’à ce que le reste ne contienne qu’un élément et dans ce cas la liste renvoyée est très courte, elle ne contient qu’un élément le fameux élément restant.
4. On combine l’élément choisi avec toutes les permutations du reste.

Mini-Application 1 : Les Arrangements de Mots ✍️

Essayez de compléter cette fonction pour qu’elle affiche toutes les permutations d’une chaîne de caractères (par exemple, « ABC »).

Python

def permuter(chaine):
    if len(chaine) == 1:
        return [chaine]
    
    permutations = []
    for i, char in enumerate(chaine):
        # On choisit un caractère
        reste = chaine[:i] + chaine[i+1:] # Le reste de la chaîne
        
        # On permute le reste
        permutations_restantes = permuter(reste)
        
        # On combine le caractère choisi avec les permutations du reste
        for p_reste in permutations_restantes:
            permutations.append(char + p_reste)
            
    return permutations

print(permuter("ABC"))

C’est un peu plus complexe, mais ça montre bien la puissance de la récursivité pour découper un gros problème en petits morceaux !

🎨 La Beauté des Fractales avec Turtle 🐢

La récursivité est la reine des fractales, ces formes géométriques complexes qui se répètent à l’infini à différentes échelles. Le flocon de Koch est un exemple magnifique.

Mini-Challenge 4 : Le Flocon Magique ❄️

Regardez cette vidéo sur le flocon de Koch (ou cherchez « flocon de Koch animation » si le lien ne marche pas).

Ensuite, analysez et testez le code suivant. Concentrez-vous sur les paramètres longueur et n (le nombre d’étapes de récursivité).

Python

import turtle as t

t.speed(0) # Vitesse maximale pour un dessin rapide
t.penup()
t.goto(-150, 90) # Position de départ pour que le flocon soit bien centré
t.pendown()

def koch(longueur, n):
    if n == 0:
        t.forward(longueur)
    else:
        # Chaque segment est remplacé par 4 segments plus petits
        koch(longueur / 3, n - 1)
        t.left(60)
        koch(longueur / 3, n - 1)
        t.right(120)
        koch(longueur / 3, n - 1)
        t.left(60)
        koch(longueur / 3, n - 1)

def flocon(taille, etape):
    for _ in range(3): # Un flocon est composé de 3 segments de Koch
        koch(taille, etape)
        t.right(120)

flocon(300, 4) # Essayez différentes valeurs pour taille et etape !
t.done() # Garde la fenêtre ouverte

Le secret du flocon de Koch réside dans la fonction koch : si n est 0, on dessine juste un segment droit. Sinon, on remplace ce segment par 4 segments plus petits, en tournant de 60 ou 120 degrés, et on appelle koch récursivement pour chacun de ces segments ! C’est le principe des fractales : une petite partie ressemble au tout.

Fin du cours

Défi 1 : Le Compteur d’Étoiles Filantes 🌠

Imaginez que chaque nuit, le nombre d’étoiles filantes que vous voyez est la somme du nombre d’étoiles vues la veille, la veille de la veille, etc., jusqu’à la première nuit où vous n’en avez vu qu’une seule !

Exercice : Créez une fonction récursive nommée compte_etoiles_filantes(jour) qui calcule le nombre cumulé d’étoiles filantes observées jusqu’à un certain jour. Par définition, au jour 0, vous avez vu 1 étoile filante. Pour tout jour n > 0, le nombre d’étoiles est n s’ajoute au nombre d’étoiles des jour n-1 jusqu’à 0.

Prérequis : Maîtrise des concepts de base des fonctions (définition, appel, return). Voir la Correction du Défi 1

Analyse du problème : La définition nous est donnée :

• Cas de base : compte_etoiles_filantes(0) doit retourner 1.
• Cas récursif : compte_etoiles_filantes(n) doit retourner n + compte_etoiles_filantes(n-1).

Code :

Python

def compte_etoiles_filantes(jour):
    """
    Calcule le nombre cumulé d'étoiles filantes jusqu'à un certain jour.
    jour (int): Le numéro du jour (>= 1).
    Retourne (int): Le nombre cumulé d'étoiles.
    """
    if jour == 1:  # Cas de base : au jour 1, on a vu 1 étoile.
        return 1
    else:  # Cas récursif : le nombre d'étoiles jusqu'au jour n est (n + le nombre d'étoiles vues jusqu'au jour n-1).
        return jour + compte_etoiles_filantes(jour - 1)

# Tests rapides :
print(f"Étoiles au jour 1 : {compte_etoiles_filantes(2)}")  # Attendu : 3 (2 + 1)
print(f"Étoiles au jour 3 : {compte_etoiles_filantes(3)}")  # Attendu : 6 (3 + 2 + 1)
print(f"Étoiles au jour 5 : {compte_etoiles_filantes(5)}")  # Attendu : 15 (5 + 4 + 3 + 2 + 1 )

Défi 2 : La Danse des insectes de Syracuse 🐜

Imaginez un insecte magicien. Chaque jour, si son nombre de pattes est pair, il en perd la moitié. Si son nombre de pattes est impair, son nombre de pattes triple et gagne une patte supplémentaire en prime. La légende dit que toutes les fourmis finissent toujours par n’avoir qu’une seule patte.

Exercice : Écrivez une fonction récursive danse_syracuse(nombre_pattes) qui prend en paramètre le nombre de pattes initial de l’insecte et affiche la séquence des nombres de pattes jour après jour, jusqu’à ce que l’insecte n’en ait plus qu’une. On supposera nombre_pattes est un entier positif strictement supérieur à 1.

Prérequis : Maîtrise des opérateurs modulo (%) et division entière (//). Comprendre l’importance du cas de base pour éviter la récursion infinie.

Analyse du problème : La suite de Syracuse est définie par deux règles :

• Si u_n est pair : u_{n+1} = u_n / 2
• Si u_n est impair : u_{n+1} = 3 * u_{n} + 1 Le cas de base est lorsque u_{n] atteint 1.

Code :

Python

def danse_syracuse(nombre_pattes):
    """
    Affiche la séquence des nombres de pattes d'un insecte  de Syracuse.
    nombre_pattes (int): Le nombre de pattes actuel de l'insecte  (doit être > 1).
    """
    print(nombre_pattes)  # On affiche le nombre de pattes actuel

    if nombre_pattes == 1:  # Cas de base : l'insecte n'a plus qu'une patte
        return
    
    if nombre_pattes % 2 == 0:  # Si le nombre de pattes est pair
        danse_syracuse(nombre_pattes // 2)
    else:  # Si le nombre de pattes est impair
        danse_syracuse(3 * nombre_pattes + 1)

# Tests rapides :
print("Séquence pour 6 :")
danse_syracuse(6)
# Attendu : 6 3 10 5 16 8 4 2 1

print("\nSéquence pour 27 :")
danse_syracuse(27)
# La séquence est plus longue, mais doit finir par 1.

Défi 3 : La suite des Nombres Étranges 🎶

Imaginez une suite où chaque valeur dépend des deux valeurs précédentes et d’une constante. La première valeur est notée ‘A’ et la deuxième note est notée ‘B’. Ensuite, chaque nouvelle note est calculée en combinant trois fois la note précédente, deux fois celle d’avant et en ajoutant cinq .

Exercice : Écrivez une fonction récursive suite_etrange(n, note_A, note_B) qui renvoie la valeur de la n-ième note de cette suite, en considérant que n=0 correspond à note_A et n=1 à note_B.

Prérequis : Compréhension des suites définies par récurrence sur plusieurs termes précédents.

Analyse du problème : La suite est définie par :

• u_0 = a
• u_1 = b
• u_n = 3 * u_{n-1} + 2 * u_{n-2} + 5 pour n >= 2

Les cas de base sont n=0 et n=1. Pour les autres n, c’est un appel récursif.

Code :

Python

def suite_etrange(n, note_A, note_B):
    """
    Renvoie le n-ième terme d'une suite récursive avec deux cas de base.
    n (int): L'indice du terme à calculer (>= 0).
    note_A (float/int): La valeur du terme u_0.
    note_B (float/int): La valeur du terme u_1.
    Retourne (float/int): Le n-ième terme de la suite.
    """
    if n == 0:  # Premier cas de base
        return note_A
    elif n == 1:  # Deuxième cas de base
        return note_B
    else:  # Cas récursif
        return 3 * suite_etrange(n - 1, note_A, note_B) + 2 * suite_etrange(n - 2, note_A, note_B) + 5

# Tests rapides :
print(f"Mélodie à l'indice 0 (A=10, B=20): {melodie_etrange(0, 10, 20)}") # Attendu : 10
print(f"Mélodie à l'indice 1 (A=10, B=20): {melodie_etrange(1, 10, 20)}") # Attendu : 20
print(f"Mélodie à l'indice 2 (A=10, B=20): {melodie_etrange(2, 10, 20)}") # Attendu : 3*20 + 2*10 + 5 = 85
print(f"Mélodie à l'indice 3 (A=10, B=20): {melodie_etrange(3, 10, 20)}") # Attendu : 3*85 + 2*20 + 5 = 300

Défi 4 : Le Labyrinthe des Chiffres Croissants 🔢➡️🔢

Imaginez que vous êtes dans un labyrinthe où chaque pièce est un chiffre. Vous ne pouvez avancer que vers des pièces avec un chiffre plus élevé, et vous voulez visiter toutes les pièces entre un point de départ et un point d’arrivée.

Exercice : Créez une fonction récursive explore_labyrinthe(depart, arrivee) qui affiche tous les entiers de depart à arrivee (inclus), dans l’ordre croissant.

Prérequis : Maîtrise des opérateurs de comparaison et des structures conditionnelles (if). Voir la Correction du Défi 4

Analyse du problème : Le cas de base est lorsque depart dépasse arrivee. Sinon, on affiche depart et on explore le reste du labyrinthe en augmentant depart.

Code :

Python

def explore_labyrinthe(depart, arrivee):
    """
    Affiche tous les entiers entre depart et arrivee (inclus) dans l'ordre.
    depart (int): L'entier de départ.
    arrivee (int): L'entier d'arrivée.
    """
    if depart > arrivee:  # Cas de base : on a dépassé l'arrivée
        return
    else:  # Cas récursif
        print(depart, end=" ") # Afficher l'entier actuel
        explore_labyrinthe(depart + 1, arrivee) # Appeler la fonction pour l'entier suivant

# Tests rapides :
print("Exploration de 0 à 3 :")
explore_labyrinthe(0, 3) # Attendu : 0 1 2 3
print("\nExploration de 5 à 5 :")
explore_labyrinthe(5, 5) # Attendu : 5
print("\nExploration de 7 à 4 :")
explore_labyrinthe(7, 4) # Attendu : rien (condition depart > arrivee est vraie immédiatement)

Défi 5 : Le Décodeur de Clés Secrètes (PGCD) 🔑

Pour déverrouiller une porte secrète, vous avez besoin du plus grand commun diviseur (PGCD) de deux nombres. La machine utilise un algorithme où si le deuxième nombre est zéro, le PGCD est le premier nombre. Sinon, le PGCD est celui du deuxième nombre et du reste de la division du premier par le deuxième.

Exercice : Écrivez une fonction récursive decode_cle_secrete(a, b) qui renvoie le PGCD de deux entiers positifs a et b, en utilisant l’algorithme d’Euclide.

Prérequis : Connaissance de l’algorithme d’Euclide pour le PGCD, et de l’opérateur modulo (%).

Analyse du problème : L’algorithme d’Euclide est intrinsèquement récursif : on fait des divisions euclidiennes successives et à chaque fois le diviseur devient le nouveau dividende et le reste devient le nouveau diviseur. Du coup le PGCD de la paire de base a la même valeur que la paire suivante, qui aura la même valeur que … De plus on est censé s’arrêter et prendre le dernier reste non nul. Vérifier que tout ça peut être traduit de la manière suivante :

• Cas de base : Si b est 0, le PGCD est a.
• Cas récursif : Sinon, PGCD(a, b) = PGCD(b, a % b).

Code :

Python

def decode_cle_secrete(a, b):
    """
    Calcule le Plus Grand Commun Diviseur (PGCD) de deux entiers positifs.
    a (int): Le premier entier.
    b (int): Le deuxième entier.
    Retourne (int): Le PGCD de a et b.
    """
    if b == 0:  # Cas de base de l'algorithme d'Euclide
        return a
    else:  # Cas récursif
        return decode_cle_secrete(b, a % b)

# Tests rapides :
print(f"PGCD(48, 18) : {decode_cle_secrete(48, 18)}") # Attendu : 6
print(f"PGCD(17, 5) : {decode_cle_secrete(17, 5)}")   # Attendu : 1
print(f"PGCD(100, 25) : {decode_cle_secrete(100, 25)}") # Attendu : 25
print(f"PGCD(7, 0) : {decode_cle_secrete(7, 0)}")     # Attendu : 7

Défi 6 : L’Inspecteur de Chiffres 🕵️‍♀️

Vous êtes un inspecteur et vous devez compter le nombre de chiffres qui composent un suspect numérique. Chaque fois que vous examinez un chiffre, vous retirez ce chiffre et comptez le reste. Par exemple si vous inspectez 179, vous allez prendre 9, et il restera 17, puis vous prendrez 7, il restera 1, vous le prenez il ne reste rien. Vous avez pris successivement trois chiffres avant de ne rien avoir à prendre donc, la réponse vous allez rendre/afficher est 3. Ça à l’air simple comme ça, mais passer de 179 à 17 puis à 1 et enfin à rien, ça va vous demander un peu de réflexion.

Exercice : Écrivez une fonction récursive inspecteur_de_chiffres(n) qui prend un entier positif ou nul n et renvoie son nombre de chiffres décimaux.

Prérequis : Maîtrise des opérateurs de division entière (//). Gérer le cas n=0 correctement.

Analyse du problème :

• Le nombre de chiffres d’un nombre entre 0 et 9 est 1. C’est notre cas de base.
• Pour un nombre n plus grand, le nombre de chiffres est 1 (pour le chiffre des unités) plus le nombre de chiffres de n // 10.

Code :

Python

def inspecteur_de_chiffres(n):
    """
    Renvoie le nombre de chiffres décimaux d'un entier positif ou nul.
    n (int): L'entier à analyser (>= 0).
    Retourne (int): Le nombre de chiffres.
    """
    if n < 10:  # Cas de base : si n est un chiffre (0-9)
        return 1
    else:  # Cas récursif : retirer le dernier chiffre et compter le reste
        return 1 + inspecteur_de_chiffres(n // 10)

# Tests rapides :
print(f"Chiffres de 0 : {inspecteur_de_chiffres(0)}")      # Attendu : 1
print(f"Chiffres de 7 : {inspecteur_de_chiffres(7)}")      # Attendu : 1
print(f"Chiffres de 42 : {inspecteur_de_chiffres(42)}")     # Attendu : 2
print(f"Chiffres de 12345 : {inspecteur_de_chiffres(12345)}") # Attendu : 5

Défi 7 : Le Compteur de Bits Lumineux 💡

Dans le monde binaire, certains bits sont « lumineux » (valent 1) et d’autres sont « éteints » (valent 0). Vous devez compter combien de bits lumineux il y a dans la représentation binaire d’un nombre.

Exercice : Écrivez une fonction récursive compteur_bits_lumineux(n) qui prend un entier positif ou nul n et renvoie le nombre de bits valant 1 dans sa représentation binaire.

Prérequis : Connaissance des opérateurs binaires (% 2 pour le dernier bit, // 2 pour décaler à droite). Voir la Correction du Défi 7

Analyse du problème :

• Le cas de base est lorsque n est 0, il n’y a aucun bit 1.
• Pour n > 0, on vérifie le dernier bit (n % 2). S’il vaut 1, on l’ajoute au compte. Ensuite, on compte les bits 1 dans le reste du nombre (n // 2).

Code :

Python

def compteur_bits_lumineux(n):
    """
    Renvoie le nombre de bits valant 1 dans la représentation binaire d'un entier.
    n (int): L'entier positif ou nul.
    Retourne (int): Le nombre de bits à 1.
    """
    if n == 0:  # Cas de base : plus de bits à examiner
        return 0
    else:  # Cas récursif
        # On ajoute 1 si le dernier bit est 1 (n % 2)
        # Puis on compte les bits 1 dans le reste du nombre (n // 2)
        return (n % 2) + compteur_bits_lumineux(n // 2)

# Tests rapides :
print(f"Bits lumineux de 0 (0b0) : {compteur_bits_lumineux(0)}")      # Attendu : 0
print(f"Bits lumineux de 1 (0b1) : {compteur_bits_lumineux(1)}")      # Attendu : 1
print(f"Bits lumineux de 2 (0b10) : {compteur_bits_lumineux(2)}")     # Attendu : 1
print(f"Bits lumineux de 3 (0b11) : {compteur_bits_lumineux(3)}")     # Attendu : 2
print(f"Bits lumineux de 255 (0b11111111) : {compteur_bits_lumineux(255)}") # Attendu : 8
print(f"Bits lumineux de 10 (0b1010) : {compteur_bits_lumineux(10)}")    # Attendu : 2

Défi 8 : Le Détecteur d’Intrusions dans le Tableau 🚨

Vous êtes le gardien d’un tableau de valeurs et vous devez vérifier si une valeur spécifique est présente à partir d’un certain point.

Exercice : Écrivez une fonction récursive detecteur_intrusions(valeur, tableau, indice_depart) qui renvoie True si valeur apparaît dans tableau à partir de indice_depart (inclus) jusqu’à la fin du tableau, et False sinon. On garantit que indice_depart est toujours un indice valide.

Prérequis : Maîtrise des listes/tableaux (accès par indice, len()), des opérateurs de comparaison et des booléens. Voir la Correction du Défi 8

Analyse du problème :

• Cas de base 1 : Si indice_depart atteint la fin du tableau (len(tableau)), cela signifie que la valeur n’a pas été trouvée, donc on retourne False.
• Cas de base 2 : Si la valeur à tableau[indice_depart] correspond à valeur, on a trouvé, on retourne True.
• Cas récursif : Sinon, on continue la recherche à l’indice suivant (indice_depart + 1).

Code :

Python

def detecteur_intrusions(valeur, tableau, indice_depart):
    """
    Vérifie si une valeur est présente dans un tableau à partir d'un certain indice.
    valeur (any): La valeur à rechercher.
    tableau (list): Le tableau dans lequel chercher.
    indice_depart (int): L'indice à partir duquel commencer la recherche (inclus, >=0).
    Retourne (bool): True si la valeur est trouvée, False sinon.
    """
    # Cas de base 1 : L'indice a dépassé la fin du tableau, la valeur n'est pas trouvée.
    if indice_depart == len(tableau):
        return False
    # Cas de base 2 : La valeur est trouvée à l'indice actuel.
    elif tableau[indice_depart] == valeur:
        return True
    # Cas récursif : La valeur n'est pas à l'indice actuel, on cherche dans le reste du tableau.
    else:
        return detecteur_intrusions(valeur, tableau, indice_depart + 1)

# Tests rapides :
mon_tableau = [10, 20, 30, 40, 50]
print(f"20 dans [10, 20, 30, 40, 50] à partir de 0 : {detecteur_intrusions(20, mon_tableau, 0)}") # Attendu : True
print(f"60 dans [10, 20, 30, 40, 50] à partir de 0 : {detecteur_intrusions(60, mon_tableau, 0)}") # Attendu : False
print(f"40 dans [10, 20, 30, 40, 50] à partir de 3 : {detecteur_intrusions(40, mon_tableau, 3)}") # Attendu : True
print(f"10 dans [10, 20, 30, 40, 50] à partir de 1 : {detecteur_intrusions(10, mon_tableau, 1)}") # Attendu : False
print(f"50 dans [10, 20, 30, 40, 50] à partir de 4 : {detecteur_intrusions(50, mon_tableau, 4)}") # Attendu : True

Défi 9 : Le Secret du Triangle Magique de Pascal 🧙‍♂️

Le triangle de Pascal est un artefact mathématique où chaque nombre est la somme des deux nombres directement au-dessus de lui. Les bords du triangle sont toujours des 1.

Exercice :

1. Écrivez une fonction récursive coefficient_magique(n, p) qui renvoie la valeur du coefficient binomial C(n,p) (le nombre à la ligne n et à la position p dans le triangle de Pascal), en utilisant la définition récursive donnée :
   • C(n,p)=1 si p=0 ou n=p
   • C(n,p)=C(n−1,p−1)+C(n−1,p) sinon.
2. Utilisez une double boucle for pour afficher les 11 premières lignes (de n=0 à n=10) du triangle de Pascal, en utilisant votre fonction.

Prérequis : Maîtrise des boucles for imbriquées et de l’affichage formaté (print). Comprendre la définition mathématique récursive. Voir la Correction du Défi 9

Analyse du problème : La définition récursive est très claire :

• Cas de base 1 : p = 0, le coefficient est 1.
• Cas de base 2 : n = p, le coefficient est 1.
• Cas récursif : C(n-1, p-1) + C(n-1, p).

Code :

Python

def coefficient_magique(n, p):
    """
    Calcule le coefficient binomial C(n, p) du triangle de Pascal de manière récursive.
    n (int): Le numéro de la ligne (>= 0).
    p (int): La position dans la ligne (0 <= p <= n).
    Retourne (int): La valeur du coefficient C(n, p).
    """
    if p == 0 or n == p:  # Cas de base : les bords du triangle
        return 1
    else:  # Cas récursif : somme des deux éléments au-dessus
        return coefficient_magique(n - 1, p - 1) + coefficient_magique(n - 1, p)

# Tests rapides de la fonction :
print(f"C(0, 0) : {coefficient_magique(0, 0)}")  # Attendu : 1
print(f"C(3, 1) : {coefficient_magique(3, 1)}")  # Attendu : 3
print(f"C(4, 2) : {coefficient_magique(4, 2)}")  # Attendu : 6

# Dessin du triangle de Pascal
print("\n--- Triangle Magique de Pascal (jusqu'à n=10) ---")
for n_ligne in range(11):  # Pour chaque ligne de 0 à 10
    # Optionnel : pour centrer l'affichage (ajuster selon la taille de la console)
    print(" " * (10 - n_ligne), end="")
    for p_position in range(n_ligne + 1):  # Pour chaque position dans la ligne
        print(f"{coefficient_magique(n_ligne, p_position):4d}", end="") # :4d pour aligner
    print() # Passer à la ligne suivante

Défi 10 : Retour sur les autres fractales

Faites une petite recherche sur les fractales de Sierpinsky.

Est ce que l’image fournie par l’IA est réaliste ? Etudier d’un peu plus près la logique derrière les deux fractales.

Exercice :

Créer deux programmes pour les deux versions de la fractale

Analyse du problème et conseils : on peut créer une fonction dessinant le motif de base : un triangle équilatéral / rectangle.

les coordonnées d’un triangle équilatéral de côté l et dont le premier sommet a pour coordonnées (0,0) seront (0,0) , (l,0) et (l/2,racine(3)/2).

pour le triangle de Sierpinski voici un début de programme :

from turtle import *
from math import sqrt

speed(0) # Vitesse maximale pour un dessin rapide

def triangle(x:int,y:int,l:int,c:str):
    """dessine un triangle équilatéral de dimension l et de couleur c
    il aura une base horizontale et la pointe vers le haut"""
    penup()
    goto(x,y) # Position de départ pour le rectangle
    pendown()
    fillcolor(c)
    begin_fill()
    forward(l)
    left(120)
    forward(l)
    left(120)
    forward(l)
    left(120)
    end_fill()

def SierTri(x,y,l,c1,c2,n):
    """dessine le triangle de Sierpinski de dimension l à l'ordre n,
    son premier sommet a pour coordonnées (x,y), c1 est la couleur majoritaire
    c2 est celle des incrustations"""
    if n==0 :
        triangle(x,y,l,c1)
    else :
        triangle(x,y,l,c2) #l'incrustation apparaitra par transparence
        SierTri(x,y,l/2,c1,c2,n-1)
        SierTri(x+l/2,y,l/2,c1,c2,n-1)
        SierTri(x+l/4,y+sqrt(3)*l/4,l/2,c1,c2,n-1)

def SierCent(l,c1,c2,n) :
    SierTri(-l/2,-sqrt(3)*l/4,l,c1,c2,n)

SierCent(200,"blue","red",4)
done() # Garde la fenêtre ouverte

• Pour le tapis, un peu moins d’aide est nécessaire,

from turtle import *

def rectangle(x,y,h,l,c):
    penup()
    goto(x,y) # Position de départ pour le rectangle
    pendown()
    fillcolor(c)
    begin_fill()
    forward(l)
    right(90)
    forward(h)
    right(90)
    forward(l)
    right(90)
    forward(h)
    right(90)
    end_fill()

def Sierpinsky(x,y,h,l,c1,c2,n):
    if n==0 :
        rectangle(x,y,h,l,c1)
    else :
        Sierpinsky(x,y,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x+l/3,y,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x+2*l/3,y,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x,y-h/3,h/3,l/3,c1,c2,n-1)
        rectangle(x+l/3,y-h/3,h/3,l/3,c2)
        Sierpinsky(x+2*l/3,y-h/3,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x,y-2*h/3,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x+l/3,y-2*h/3,h/3,l/3,c1,c2,n-1)
        Sierpinsky(x+2*l/3,y-2*h/3,h/3,l/3,c1,c2,n-1)

speed(0) # Vitesse maximale pour un dessin rapide
Sierpinsky(-200,200,400,400,"blue","red",4)
done() # Garde la fenêtre ouverte

🚀 Étendre vos Horizons : Quand utiliser la Récursivité ?

disque sur un petit.

Mini-Application 2 : Le Déplaceur de Disques 💿

Recherchez les « Tours de Hanoï algorithme récursif » et essayez d’implémenter une fonction Python qui affiche les étapes pour déplacer les disques.

Python

def hanoi(n, source, cible, auxiliaire):
    if n == 1:
        print(f"Déplacer le disque 1 de {source} vers {cible}")
    else:
        hanoi(n - 1, source, auxiliaire, cible)
        print(f"Déplacer le disque {n} de {source} vers {cible}")
        hanoi(n - 1, auxiliaire, cible, source)

# Exemple : résoudre pour 3 disques
hanoi(3, "A", "C", "B")